考点:组合图形的面积
专题:平面图形的认识与计算
分析:(1)阴影部分的面积=梯形的面积-半圆的面积;圆的半径为:(8÷2)厘米;梯形的高等于圆的半径,根据梯形、圆的面积公式解答即可.
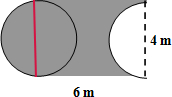
(2)把左边的半圆割补到右边空白半圆处,则阴影部分的面积=长方形的面积(长为6米、宽为4米);
阴影部分的周长=直径为4米的圆的周长+两条长为6米的边;根据圆的周长公式:C=πd,解答即可.
解答:
解:(1)(8+12)×(8÷2)×2-3.14×(8÷2)2÷2
=40-25.12
=14.88(平方厘米)
答:阴影部分的面积是14.88平方厘米.
(2)阴影部分的面积:
6×4=24(平方米)
阴影部分的周长:
3.14×4+6×2
=12.56+12
=24.56(米)
答:阴影部分的面积是24平方米;周长为24.56米.
点评:(1)此题考查组合图形面积的计算方法,一般都是转化到规则图形中利用面积公式计算解答.
(2)分析图形,根据图形特点进行割补,寻求问题突破点.

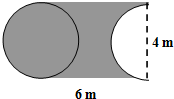
 (2)
(2)



 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案