Question

19．一个长方形和一个正方形相连（如图），甲三角形面积比乙三角形面积大多少平方分米？（单位：分米）

Answer 1

分析 首先根据CD∥AB，求出CH的长度，进而求出DH的长度是多少；然后根据MF∥CE，求出MG的长度是多少，进而求出MF的长度是多少；最后根据三角形的面积公式，分别求出甲三角形面积、乙三角形面积各是多少平方分米，再把它们求差即可．

解答 解：如图，，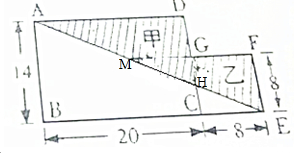
因为CD∥AB，
所以$\frac{CH}{AB}=\frac{CE}{BE}=\frac{8}{8+20}=\frac{2}{7}$，
所以CH=14×$\frac{2}{7}=4（分米）$，DH=CD-CH=14-4=10（分米）；
因为MF∥CE，
所以$\frac{MG}{CE}=\frac{GH}{CH}=\frac{8-4}{4}=1$，
所以MG=CE=8（分米），MF=8+8=16（分米）；
20×10÷2-16×8÷2
=100-64
=36（平方分米）
答：甲三角形面积比乙三角形面积大36平平方分米．

点评 此题主要考查了组合图形的面积的求法，要熟练掌握，解答此题的关键是熟练掌握三角形的面积公式，求出甲三角形面积、乙三角形面积各是多少平方分米．