
 化成小数,小数部分第100位上的数是______.
化成小数,小数部分第100位上的数是______. ;若给它的分母减去2,可化简为
;若给它的分母减去2,可化简为 .那么原来这个分数是______.
.那么原来这个分数是______. =
= =4;
=4; =2.
=2. 4285
4285 ,
, ,
, ,所以a=
,所以a= ,
, =
= ,所以a=4b+2,
,所以a=4b+2, =4b+2,两边同时乘3,
=4b+2,两边同时乘3,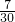 .
.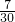 .
. 化成小数,再看它的循环节是几位数,用100除以循环周期,如果能整除则是直接的末位数字,如果有余数,余数是几就从循环节的首位数出第几位,该位上数字即是所求数字.
化成小数,再看它的循环节是几位数,用100除以循环周期,如果能整除则是直接的末位数字,如果有余数,余数是几就从循环节的首位数出第几位,该位上数字即是所求数字. ,根据“若分子加上2,约分后为
,根据“若分子加上2,约分后为  ”,原分数就变为
”,原分数就变为 ,与
,与 相等;再根据“若分母减去2,约分后为
相等;再根据“若分母减去2,约分后为  ”,原分数就变为
”,原分数就变为 ,与
,与 相等;把这两个方程进一步转化为是求一个未知数的方程,进而求得分子和分母的数值,问题得解.
相等;把这两个方程进一步转化为是求一个未知数的方程,进而求得分子和分母的数值,问题得解.

 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案科目:小学数学 来源: 题型:
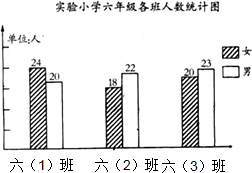
查看答案和解析>>
科目:小学数学 来源: 题型:
| ? |
| 1 |
| ? |
| 8 |
| ? |
| 1 |
| ? |
| 8 |
查看答案和解析>>
科目:小学数学 来源: 题型:
查看答案和解析>>
科目:小学数学 来源: 题型:
 学校为在“庆祝中华人民共和国成立六十一周年金秋艺术节”中获奖的同学买奖品,共买了25份,用去人民币140元,一等奖、二等奖的奖品各买了几份?
学校为在“庆祝中华人民共和国成立六十一周年金秋艺术节”中获奖的同学买奖品,共买了25份,用去人民币140元,一等奖、二等奖的奖品各买了几份?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com