
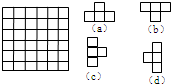 在6×6的正方形棋盘格中,请填上1~36这36个自然数,使得在任意的(a),(b),(c),(d)四种形状的图形中,放置的四个数的和都是偶数.若能,请填出一例;若不能,请说明理由.
在6×6的正方形棋盘格中,请填上1~36这36个自然数,使得在任意的(a),(b),(c),(d)四种形状的图形中,放置的四个数的和都是偶数.若能,请填出一例;若不能,请说明理由. 解:假设题设的填数法存在,那么在如右图的十字型中,由(a)有a1+a2+a3+a4是偶数;由(c)有a1+a3+a4+a5是偶数,
解:假设题设的填数法存在,那么在如右图的十字型中,由(a)有a1+a2+a3+a4是偶数;由(c)有a1+a3+a4+a5是偶数,

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com