
| 正方形的对角线长 | 2 | 4 | 6 | 8 |
| 正方形的面积 | ||||
| 外接圆的面积 | ||||
| 外接圆的面积与正方形面积的比 |
分析 (1)由题意,正方形面积是由4个同样的等腰直角三角形面积组成,直角边是正方形对角线长的一半,据此可求出正方形的面积;正方形外接圆的半径是正方形对角线长的一半,据此可求出正方形外接圆的面积,再根据比的意义写出它们的比,再化简.
(2)可任选一正方形,如角线长为2a的正方形面积是:2a×2a÷2×4=8a2,外接圆面积是:π×(2a)2=4πa2,它们的面积之比是:(4πa2):(8a2)=π:2,由此得出结论:正方形外接圆与正方形面积的比是π:2.
解答 解:(1)当正方形对角线长为2是时,2÷2=1,正方形面积:1×1÷2×4=2,外接圆面积:π×12=π,外接圆与正方形面积的比是π:2;
当正方形对角线长为4时,4÷2=2,正方形面积:2×2÷2×4=8,外接圆面积:π×22=4π,外接圆与正方形面积的比是4π:8=π:2;
当正方形对角线长为6时,6÷2=3,正方形面积:3×3÷2×4=18,外接圆面积:π×32=9π,外接圆与正方形面积的比是9π:18=π:2;
当正方形对角线长为8时,8÷2=4,正方形面积:4×4÷2×4=32,外接圆面积:π×42=16π,外接圆与正方形面积的比是16π:32=π:2.
根据以上数据填表如下:
| 正方形的对角线长 | 2 | 4 | 6 | 8 |
| 正方形的面积 | 2 | 8 | 18 | 32 |
| 外接圆的面积 | π | 4π | 9π | 16π |
| 外接圆的面积与正方形面积的比 | π:2 | π:2 | π:2 | π:2 |
点评 此题考查的知识点较多,有方形的特征及面积的计算、三角面积的计算、圆面积的计算、比的意义及化简等.正方形面积根据传统求法,边长乘边长不好求,因此把它看作是由4个同样的等腰直角三角形面积组成的.


科目:小学数学 来源: 题型:解答题
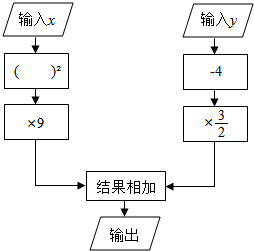 按熙下列运算程序的要求填写表:
按熙下列运算程序的要求填写表:| x | 1 | -$\frac{1}{2}$ | 0 | 2 | 1.5 |
| y | -2 | $\frac{1}{2}$ | -1 | 4 | 0.5 |
| 输出 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com