
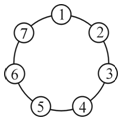
 有一颗棋子放在下图中的1号位置上,现按顺时针方向,第一次跳一步,跳到2号位置;第二次跳两步,跳到4号位置;第三次跳三步,跳到7号位置…这样一直进行下去.棋子永远跳不到的位置是3号、5号和6号.
有一颗棋子放在下图中的1号位置上,现按顺时针方向,第一次跳一步,跳到2号位置;第二次跳两步,跳到4号位置;第三次跳三步,跳到7号位置…这样一直进行下去.棋子永远跳不到的位置是3号、5号和6号. 分析 设顶点①、②、③、④、⑤、⑥、⑦分别是第0,1,2,3,4,5,6格,那么第一次跳一步到2号位置上,第二次跳两步跳到4号位置上,第三次跳三步跳到了5号位置上,依此类推可知:棋子移动了k次后走过的总格数是S=1+2+3+4+…+k=$\frac{k(1+k)}{2}$,讨论k的取值,找出不可能停棋的格子.
解答 解:设顶点①、②、③、④、⑤、⑥、⑦分别是第0,1,2,3,4,5,6格;
棋子移动了k次后走过的总格数是S=1+2+3+4+…+k=$\frac{k(1+k)}{2}$,
这里S是整数,且使0≤S≤6,分别取k=1,2,3,4,5,6,7,…时,S=1,3,6,3,1,0,0,…
是按照:1、3、6、3、1、0、0…循环的,在第2,4,5格没有停棋;
即3号、5号和6号没有停棋.
答:棋子永远跳不到的位置是3号、5号和6号.
故答案为:3号、5号和6.
点评 考查图形的规律性变化;根据棋子跳的总路程得到落脚处是解决本题的难点.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:小学数学 来源: 题型:解答题
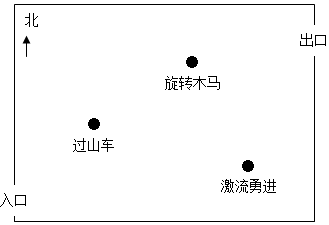 在下面游乐场设计图中,请你按要求分别做一做.
在下面游乐场设计图中,请你按要求分别做一做.查看答案和解析>>
科目:小学数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com