
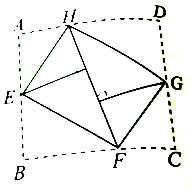
 如图所示,将矩形纸片ABCD的四个角向内折起,恰好拼成一个无缝隙、无重叠的四边形EFGH,若EH=12cm,EF=16cm,则边AD的长是20cm.
如图所示,将矩形纸片ABCD的四个角向内折起,恰好拼成一个无缝隙、无重叠的四边形EFGH,若EH=12cm,EF=16cm,则边AD的长是20cm. 分析 观察图形可知,边AD的长等于HF的长,根据勾股定理即可求得边AD的长.
解答 解:在Rt△HEF中,EH=12cm,EF=16cm,
HF=$\sqrt{E{H}^{2}+E{F}^{2}}$=20(cm)
由折叠可知AD=HF=20cm
答:边AD的长是20cm.
故答案为:20cm.
点评 考查了图形的拆拼(切拼),把一个几何图形剪成几块形状相同的图形,或是把一个几何图形剪开后拼成另一种满足某种条件的图形,完成这样的图形剪拼,需要考虑图形剪开后各部分的形状、大小以及它们之间的位置关系.本题关键是理解边AD的长等于HF的长.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:小学数学 来源: 题型:计算题
| 1.29+3.7+0.71+6.3 | 125×89×8 | 57×101-57 | 24×25×4 |
| 125×26+125×22 | 52×104 | 1569-(569+815) | 7.56-(1.56+3.72) |
查看答案和解析>>
科目:小学数学 来源: 题型:计算题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com