
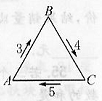
 一只蚂蚁沿边长为240cm的等边三角形ABC的三条边由A点顺时针爬行一周.它在三条边上的速度分别是每秒3cm,4cm,5cm(如图).且当它到达拐点(A,B,C)时会休息26秒,当它爬完一周回到点A时,行程结束.这期间,蚂蚁的平均速度是
一只蚂蚁沿边长为240cm的等边三角形ABC的三条边由A点顺时针爬行一周.它在三条边上的速度分别是每秒3cm,4cm,5cm(如图).且当它到达拐点(A,B,C)时会休息26秒,当它爬完一周回到点A时,行程结束.这期间,蚂蚁的平均速度是

 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:小学数学 来源: 题型:阅读理解

查看答案和解析>>
科目:小学数学 来源: 题型:
| 2 |
| 3 |
| 2 |
| 3 |
查看答案和解析>>
科目:小学数学 来源: 题型:
 用边长为1厘米的正方形瓷砖,黑白相间,铺成一个4×6的矩形(如图).一只蚂蚁从左上角的A点的出发沿正方形的边爬到右下角的B点.如果蚂蚁在爬行中,它的左边必须始终是黑色的瓷砖,那么蚂蚁至少爬行了
用边长为1厘米的正方形瓷砖,黑白相间,铺成一个4×6的矩形(如图).一只蚂蚁从左上角的A点的出发沿正方形的边爬到右下角的B点.如果蚂蚁在爬行中,它的左边必须始终是黑色的瓷砖,那么蚂蚁至少爬行了查看答案和解析>>
科目:小学数学 来源: 题型:填空题
 一只蚂蚁沿边长为240cm的等边三角形ABC的三条边由A点顺时针爬行一周.它在三条边上的速度分别是每秒3cm,4cm,5cm(如图).且当它到达拐点(A,B,C)时会休息26秒,当它爬完一周回到点A时,行程结束.这期间,蚂蚁的平均速度是________cm/s.
一只蚂蚁沿边长为240cm的等边三角形ABC的三条边由A点顺时针爬行一周.它在三条边上的速度分别是每秒3cm,4cm,5cm(如图).且当它到达拐点(A,B,C)时会休息26秒,当它爬完一周回到点A时,行程结束.这期间,蚂蚁的平均速度是________cm/s.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com