解:
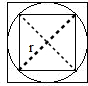
设圆的半径为r,
则大正方形的面积为:2r×2r=4r
2(平方厘米),
小正方形的面积为:2r×r÷2×2=2r
2(平方厘米),
圆的半径为:
4r
2-2r
2=10,
2r
2=10,
r
2=5,
两正方形之间圆的面积为:
πr
2-2r
2=3.14×5-2×5,
=15.7-10,
=5.7(平方厘米),
答:两正方形之间圆的面积是5.7平方厘米.
分析:由图意可知:大正方形的面积-正方形的面积=10,这个最大圆的直径应该等于小正方形的对角线的长度,最大圆的直径等于大正方形的边长,可设圆的半径为r,然后计算出大正方形和小正方形各自的面积,从而可以计算出圆的半径的平方,两正方形之间圆的面积等于圆的面积减去小正方形的面积,列式解答即可得到答案.
点评:解答此题的关键是用圆的半径表示出正方形的面积,再利用等量代换即可逐步求解.

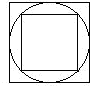 75.如图所示,大正方形的面积比小正方形的面积多1O平方厘米.求两正方形之间的圆面积.
75.如图所示,大正方形的面积比小正方形的面积多1O平方厘米.求两正方形之间的圆面积.


 53随堂测系列答案
53随堂测系列答案