Question

如图中三个阴影部分的面积（　　）最大．

• A、长方形
• B、圆
• C、梯形

Answer 1

考点：面积及面积的大小比较

专题：平面图形的认识与计算

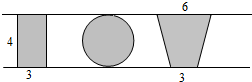
分析：由图可知长方形的长为4，宽为3；圆的直径为4，梯形的上底为6，下底为3，高为4，再根据长方形面积=长×宽求出长方形的面积，根据圆的直径求出半径，再根据圆的面积=πr²求出圆的面积，根据梯形的面积=（上底+下底）×高÷2求出梯形面积，然后比较他们的面积即可．

解答： 解：长方形的面积为：4×3=12，
圆的面积为：3.14×（4÷2）²
=3.14×4
=12.56，
梯形的面积为：（3+6）×4÷2
=9×4÷2
=18，
所以梯形的面积最大．
故选：C．

点评：此题主要根据平行线的性质，得出长方形、梯形的高与圆的直径相等，再根据长方形、圆和梯形的面积计算公式进行分析、比较即可．