
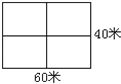
【题目】在一个长方形人工湖的中间修了两条分别为40米、60米的坝,(如右图)如果再在湖的四周和堤坝上隔2米种一棵树,最多可以种树多少棵?
【答案】147棵
【解析】
试题分析:(1)先求出四周要植树多少棵,考虑最多情况:四个角都植树,那么植树的棵树=间隔数,使四周植树棵树最多为:(40+60)×2÷2=100(棵).
(2)再求出中间两条坝上植树的棵树:因为坝的两端处在四周的中点上,所以不再植树,那么植树的棵树=间隔数﹣1,由此可以求得植树:60÷2﹣1+40÷2﹣1=48棵,中间1棵重复加了,所以两条坝上的植树棵树为:48﹣1=47棵.
由上述分析即可得出植树的总棵树.
解:四周植树棵树为:
(40+60)×2÷2,
=100×2÷2,
=100(棵).
两条坝上的植树棵树为:
60÷2﹣1+40÷2﹣1﹣1,
=30﹣1+20﹣1﹣1,
=47(棵),
100+47=147(棵);
答:最多可以种147棵树.


 科学实验活动册系列答案
科学实验活动册系列答案科目:小学数学 来源: 题型:
【题目】动手实践.
(每个小正方形边长为1cm)
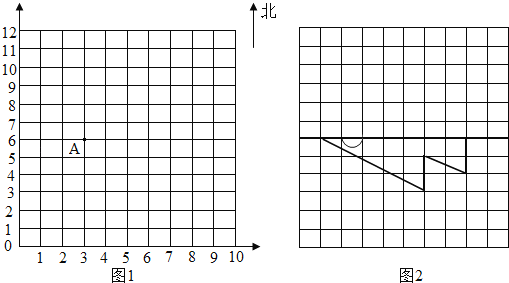
(1)如图1三角形的一个顶点A的位置在( , ).
(2)三角形的顶点B在顶点A的正东方向4cm处,位置是( , ),顶点C在顶点A的正北方向,三角形ABC的面积是6cm2,顶点C的位置是( , ),请在图中描出B点和C点,并依次连成封闭图形.
(3)将三角形ABC向下平移5cm.
(4)根据对称轴画出如图2中图形的另一半.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com