
【题目】已知函数![]() .
.
(1)曲线![]() 在点
在点![]() 处的切线平行于
处的切线平行于![]() 轴,求实数
轴,求实数![]() 的值;
的值;
(2)记![]() .
.
()讨论![]() 的单调性;
的单调性;
(ⅱ)若![]() ,
, ![]() 为
为![]() 在
在![]() 上的最小值,求证:
上的最小值,求证: ![]() .
.
【答案】(1) ![]() ;(2)答案见解析;(3)证明见解析.
;(2)答案见解析;(3)证明见解析.
【解析】试题分析:(1)先求出![]() ,由
,由 ![]() 可得
可得![]() ;(2)化简
;(2)化简![]() ,求出)
,求出)![]() ,(ⅰ)讨论
,(ⅰ)讨论![]() 时,
时, ![]() 两种情况,分别令
两种情况,分别令![]() 求得
求得![]() 的范围,可得函数
的范围,可得函数![]() 增区间,
增区间, ![]() 求得
求得![]() 的范围,可得函数
的范围,可得函数![]() 的减区间,(ⅱ)若
的减区间,(ⅱ)若![]() ,
, ![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增.
单调递增. ![]() ,令
,令![]() ,只需利用导数研究函数
,只需利用导数研究函数![]() 的单调性,求出
的单调性,求出![]() 证明其为负值即可.
证明其为负值即可.
试题解析:(1)![]()
![]()
因为![]() 在
在![]() 处的切线平行于
处的切线平行于![]() 轴,所以
轴,所以![]() ,所以
,所以![]() ;
;
(2)![]()
(ⅰ)![]()
![]()
若![]() ,即
,即![]() 时,则由
时,则由![]() 得
得![]()
当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() ;
;
所以![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增.
单调递增.
若![]() ,则由
,则由![]() 得
得![]() 或
或![]()
构造函数![]() ,则
,则![]()
由![]() 得
得![]() ,所以
,所以![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增.
单调递增.
![]() ,所以
,所以![]() (当且仅当
(当且仅当![]() 时等号成立)
时等号成立)
①若![]() 在
在![]() 单调递增.
单调递增.
②若![]() 或
或![]() ,
,
当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() ;
;
所以![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增.
单调递增.
(ⅱ)若![]() ,
, ![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增.
单调递增.
![]() ,令
,令![]()
则![]() ,令
,令![]() ,
,
![]()
![]() 在
在![]() 单调递减,
单调递减,
![]() ,
, ![]()
所以存在唯一的![]() 使得
使得![]() ,
,
所以![]() 在
在![]() 单调递增,在
单调递增,在![]() 单调递减
单调递减
故当![]() 时,
时, ![]() 又
又![]()
所以![]()
![]()
所以当![]() 时,
时, ![]()


 名校课堂系列答案
名校课堂系列答案科目:小学数学 来源: 题型:
【题目】在括号里填上“>”“<”或“=”。
44(______)41 86(_______) 86 64(______)64 100(______)98
10个十(______)40个一 5个十(______)50个十 一个百(______)99个一
60个十(______)7个十 100(______)九个十
查看答案和解析>>
科目:小学数学 来源: 题型:
【题目】括号里最大能填几?
47>(______) 90>(______) (______)<17 (______)=73
(______)<82 63>(______) (______)<54 98>(______)
查看答案和解析>>
科目:小学数学 来源: 题型:
【题目】为弘扬“中华优秀传统文化”,某中学在校内对全体学生进行了一次相关测试,规定分数大于等于80分为优秀,为了解学生的测试情况,现从近2000名学生中随机抽取100名学生进行分析,按成绩分组,得到如下的频率分布表:
分数 |
|
|
|
|
|
频数 | 5 | 35 | 30 | 20 | 10 |
(1)在图中作出这些数据的频率分布直方图;
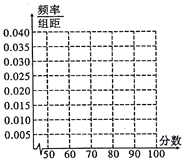
(2)估计这次测试的平均分;
(3)若这100名学生中有甲、乙两名学生,且他们的分数低于60分,现从成绩低于60的5名学生中随机选2人了解他们平时读书的情况,求甲或乙被选到的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com