
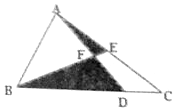
 如图,三角形ABC的面积为56平方厘米,BC=4CD,E为AC边上一点,且BE与AD的交点F是AD的中点,求阴影部分三角形面积之和.
如图,三角形ABC的面积为56平方厘米,BC=4CD,E为AC边上一点,且BE与AD的交点F是AD的中点,求阴影部分三角形面积之和. 分析 连接FC,因为F是AD的中点,所以AF=FD,三角形ABF和三角形BDF等底等高,所以三角形ABF和三角形BDF的面积相等,这样阴影部分的面积之和等于三角形ABE的面积;又因为BC=4CD,即BD:DC=(4-1):1=3:1,那么三角形BFD的面积=$\frac{3}{4}$×三角形BCF的面积,所以,三角形ABF的面积=$\frac{3}{4}$×三角形BCF的面积,则三角形ABF的面积:三角形BCF的面积=3:4,根据燕尾定律,那么AE:EC=3:4,那么三角形ABE的面积:三角形BEC的面积=3:4,那么三角形ABE的面积占三角形ABC的面积的$\frac{3}{3+4}$,然后解答即可求阴影部分的面积之和.
解答 解:连接FC,
因为F是AD的中点,所以AF=FD,三角形ABF和三角形BDF等底等高,所以三角形ABF和三角形BDF的面积相等,这样阴影部分的面积之和等于三角形ABE的面积;
又因为BC=4CD,即BD:DC=(4-1):1=3:1,那么三角形BFD的面积=$\frac{3}{4}$×三角形BCF的面积,
所以,三角形ABF的面积=$\frac{3}{4}$×三角形BCF的面积,则三角形ABF的面积:三角形BCF的面积=3:4,
根据燕尾定律,那么AE:EC=3:4,那么三角形ABE的面积:三角形BEC的面积=3:4,
那么三角形ABE的面积即阴影部分的面积之和是:
56×$\frac{3}{3+4}$
=56×$\frac{3}{7}$
=24(平方厘米);
答:阴影部分三角形面积之和是24平方厘米.
点评 本题考查了三角形面积与底的正比关系以及燕尾定律的综合应用.关键是通过图形的等积转化,求出三角形ABF的面积与三角形BCF的面积的比.


科目:小学数学 来源: 题型:计算题
查看答案和解析>>
科目:小学数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com