
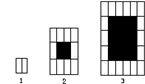
 某体育馆用大小相同的长方形木块镶嵌地面,第1次铺2块,如图1;第2次把第1次铺的完全围起来,如图2;第3次把第2次铺的完全围起来,如图3;….依此方法,(1)第5次铺完后,镶嵌所使用的木块数是34.
某体育馆用大小相同的长方形木块镶嵌地面,第1次铺2块,如图1;第2次把第1次铺的完全围起来,如图2;第3次把第2次铺的完全围起来,如图3;….依此方法,(1)第5次铺完后,镶嵌所使用的木块数是34.分析 结合图形发现:第1次镶嵌所使用的木块数为1×2=2,第2次镶嵌所使用的木块数为3×4-1×2=10,第3次镶嵌所使用的木块数为5×6-3×4=18,从数据上看,每一次镶嵌使用的木块数都比前一次多8块,推而广之即可.
解答 解:(1)观察前边的三个图形,发现,
第1次镶嵌所使用的木块数为2,
第2次镶嵌所使用的木块数为10,
第3次镶嵌所使用的木块数为18,…
所以第n次镶嵌所使用的木块数为:2+(n-1)×8=8n-6,
所以第5次镶嵌所使用的木块数为:
8×5-6=40-6=34.
答:第5次镶嵌所使用的木块数为34.
(2)用含有字母n的式子表示第n次所铺的木块数,则第n次镶嵌所使用的木块数为:
2+(n-1)×8
=2+8n-8
=8n-6
答:第n次镶嵌所使用的木块数是8n-6.
故答案为:(1)34;(2)8n-6.
点评 考查了规律型:图形的变化,此题要结合图形和数字之间的规律进行推广.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:小学数学 来源: 题型:解答题
查看答案和解析>>
科目:小学数学 来源: 题型:解答题
查看答案和解析>>
科目:小学数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com