号码分别为123,137,145,167的四名运动员进行乒乓球比赛,规定每两人比赛的盘数,是他们号码的和被3除所得的余数.那么,打球盘数最少的运动员打了________盘.
1
分析:因为每两人的号码和被3除所得的余数,等于它们各自号码被3除的余数之和被3除的余数,所以根据四名运动员的号码被3除所得的余数分别是:0,2,1,2.可以得到他们之间比赛的盘数.
解答:123÷3=41,
137÷3=45…2,
145÷3=48…1,
167÷3=55…2;
因为每两人的号码和被3除所得的余数,等于它们各自号码被3除的余数之和被3除的余数,所以根据四名运动员的号码被3除所得的余数分别是:0,2,1,2.可以得到他们之间比赛的盘数见下表:
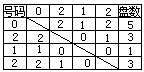
答:打球盘数最少的运动员打了 1盘.
故答案为:1.
点评:此题考查了有余数的除法.



