练习册

  • 练习册
  • 试题
    精英家教网 > 小学数学 > 题目详情

    如图，用四种不同颜色给大正方形中的A、B、C、D四个小正方形涂色，要求有相邻边的两个正方形不得涂相同颜色(无相邻边的小正方形A、C与B、D之间可以同色)．问共有多少种涂色方法？

    答案：
    解析：

    　　(1)若A、C同色，即A、C可以有4种不同的涂色方法，相应的B只能有除A(C)颜色之外的3种颜色可涂，同样D亦只能有3种涂色法．这样由乘法原理，此类情况共有4×3×3＝36种不同的涂色法．

    　　(2)若A、C不同色，A有4种不同的涂色法，则C应有3种颜色可涂，而B、D又相应各有2种涂色法，那么共有4×3×2×2＝48种不同的涂色法．依分类计数法，本题共有36＋48＝84种不同涂色法．说明：这是一道分类法和分步法的综合题


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：小学数学 来源： 题型：

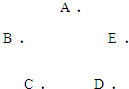    如图，平面内有A，B，C，D，E五个点，将其中每两个点都用带有颜色的线段连接起来，且满足有任意有公共端点的线段不同色．
    （1）用四种颜色的线段连接各点，能否满足题目的要求，说明理由．
    （2）至少需要几种颜色的线段，能满足题目的要求，举一例说明即可（举例时用编号代替颜色）．

    查看答案和解析>>

    科目：小学数学 来源： 题型：

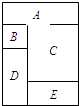    如图，把A、B、C、D、E这个五部分用四种不同的颜色着色，且相邻的部分不能使用同一种颜色，不相领的部分可以使用同一种颜色．那么这幅图一共有多少种不同的着色方法？

    查看答案和解析>>

    科目：小学数学 来源： 题型：

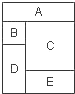    如图，把A，B，C，D，E这五部分用四种不同的颜色着色，且相邻的部分不能使用同一种颜色，不相邻的部分可以使用同一种颜色．那么，这幅图一共有
    96
    96
    种不同的着色方法．

    查看答案和解析>>

    科目：小学数学 来源： 题型：

    如图，老师要求大家用四种颜色（四种颜色可以全用也可以只选用其中几种颜色），给下面被分成了4部分的圆涂色，要求相邻部分的颜色不同，问共有多少种不同的涂法？

    查看答案和解析>>

    同步练习册答案