Question

8．将从1开始的自然数分组如图．

（1）按此规律第8行第1个数字是50，第8个数字是57，第8行所有数字的平均数是57．
（2）第n行第一个数字是n²-2n+2，最后一个数字是n²．

Answer 1

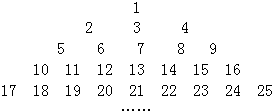
分析 （1）首先根据图示，可得每一行数字的个数分别是1、3、5、7、9、…、2n-1；然后根据等差数列的求和方法，求出前7行的数字的总数是多少；再用前7行的数字的总数分别加上1、8，求出第8行第1个数字、第8行第8个数字各是多少即可；最后根据平均数的求法，用第8行所有数字的和除以数字的个数，求出平均数是多少即可．
（2）首先根据等差数列的求和方法，求出前n-1行的数字的总数是多少；然后用前n-1行的数字的总数加上1，求出第n行第一个数字是多少；最后用前n-1行的数字的总数加上2n-1，求出最后一个数字是多少即可．

解答 解：（1）第8行第1个数字是：
（1+3+5+7+9+11+13）+1
=（1+13）×7÷2+1
=49+1
=50

第8个数字是：
（1+3+5+7+9+11+13）+8
=（1+13）×7÷2+8
=49+8
=57

第8行的数字个数是：
2×8-1=15（个），
第8行的最后一个数字是：
50+15-1=64，
第8行所有数字的平均数是：
[（50+64）×15÷2]÷15
=114×15÷2÷15
=57
答：第8行第1个数字是50，第8个数字是57，第8行所有数字的平均数是57．

（2）第n行第一个数字是：
（1+3+5+7+…+2n-3）+1
=（1+2n-3）×（n-1）÷2+1
=n²-2n+1+1
=n²-2n+2
第n行最后一个数字是：
（1+3+5+7+…+2n-3）+（2n-1）
=（1+2n-3）×（n-1）÷2+（2n-1）
=n²-2n+1+（2n-1）
=n²
答：第n行第一个数字是n²-2n+2，最后一个数字是n²．
故答案为：50、57、57；n²-2n+2、n²．

点评 （1）此题主要考查了数阵图中找规律问题的应用，注意观察总结出规律，并能正确的应用规律，解答此题的关键是要明确每一行数字的个数分别是1、3、5、7、9、…、2n-1．
（2）此题还考查了等差数列的求和公式，以及平均数的含义和求法的应用，要熟练掌握．