
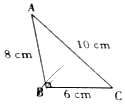
 有一个直角三角形ABC如图所示(三条边的长度在图中标出).
有一个直角三角形ABC如图所示(三条边的长度在图中标出).分析 (1)根据题意,三角形ABC绕B点旋转一周,斜边AC扫过的区域是一个环形,根据S=π(R2-r2),代入数据解答即可.
(2)首先根据题意,可得这个直角三角形绕斜边旋转一周得到的图形是一个有公共底的两个圆锥组成图形,两个圆锥的高的和等于直角三角形斜边的长;然后根据圆锥的体积公式V=$\frac{1}{3}$πr2h,用圆锥的底面积乘以直角三角形的斜边的长,再乘以$\frac{1}{3}$,即可求出此立方体图形的体积是多少.
解答 解:(1)3.14×82-3.14×62
=200.96-113.04
=87.92(平方厘米)
答:斜边AC扫过的区域的面积是87.92平方厘米.
(2)$\frac{1}{3}$π×(6×8÷10)2×10
=$\frac{1}{3}$π×4.8×4.8×10
=1.6×48×3.14
=241.152(立方厘米)
答:三角形旋转得到的立体图形的体积是241.152立方厘米.
点评 本题考查的是环形面积和圆锥体积的计算及旋转的性质,解答此题的关键是判断出旋转后的图形,并熟练掌握圆面积公式和圆锥体积公式.


科目:小学数学 来源: 题型:解答题
查看答案和解析>>
科目:小学数学 来源: 题型:选择题
| A. | 84×13÷4 | B. | 84×12×4 | C. | 84÷12×4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com