练习册

  • 练习册
  • 试题
    精英家教网 > 小学数学 > 题目详情
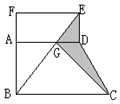
    18．如图，是长方形ADEF和直角梯形ABCD组成的组合图形，已知长方形AFED的面积是90平方厘米，求阴影部分面积．

    分析 利用等积变换思想，将所求阴影部分面积转化成一个规则的易求的几何图形的面积．首先，△GCD的面积等于△GDB的面积，而△BCE的面积等于△DEF的面积．

    解答 解：如图，连接BD．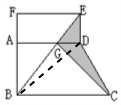


    因为AD∥BC
    所以S△GCD=S△GDB
    因为FE∥AD，
    所以S△BCE=S△DEF=$\frac{1}{2}$×90=45（平方厘米）
    即阴影部分的面积为45平方厘米．
    答：阴影部分面积是45平方厘米．

    点评 本题主要考查了三角形面积的等积变换，难度不大，但却是一道经典好题．巧妙地将所求阴影部分的面积转化成△EFD的面积是解决本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：小学数学 来源： 题型：解答题

    10．小马虎在计算一道除法算式时，把被除数末尾的一个0弄丢了，除以5后商是14，余数是2．这道除法算式的正确答案是多少？

    查看答案和解析>>

    科目：小学数学 来源： 题型：解答题

    9．根据已知条件，在相应问题的横线上写出算式，不必计算．
    利民超市运进一批大米共400袋，上午卖出总数的$\frac{1}{4}$，下午卖出总数的$\frac{1}{5}$．
    问题①：上午卖出大米多少袋？算式：400×$\frac{1}{4}$
    问题②：上午、下午一共卖出大米多少袋？算式：400×（$\frac{1}{4}$+$\frac{1}{5}$）
    问题③：还剩下大米多少袋？算式：400×（1-$\frac{1}{4}$-$\frac{1}{5}$）．

    查看答案和解析>>

    科目：小学数学 来源： 题型：填空题

    6．甲数的$\frac{2}{5}$等于乙数的$\frac{3}{4}$．如果乙数是16，那么甲数是30．

    查看答案和解析>>

    科目：小学数学 来源： 题型：计算题

    13．估算．
    25÷3≈74÷4≈82÷8≈53÷3≈
    33÷6≈76÷7≈89÷9≈46÷9≈

    查看答案和解析>>

    科目：小学数学 来源： 题型：填空题

    3．甲数是a，乙数比甲的3倍少b，乙数表示为3a-b．

    查看答案和解析>>

    科目：小学数学 来源： 题型：解答题

    10．脱式计算．
    75+20×4
    6×409-2300
    7×（1010-694）

    查看答案和解析>>

    科目：小学数学 来源： 题型：计算题

    7．脱式计算，能简算的要简算．
    2016×$\frac{2014}{2015}$               
    $\frac{1}{5}$×27+$\frac{3}{5}$×41
    6×$\frac{7}{12}$-$\frac{9}{20}$×6+$\frac{11}{30}$×6       
    19×$\frac{2}{5}$+8.2×4%-0.4．

    查看答案和解析>>

    科目：小学数学 来源： 题型：操作题

    8．甲、乙两列火车分别从两个车站同时相向而行，甲火车每小时行120千米，乙火车每小时行135千米，经过3小时两车相遇． 根据以上信息，把下面的问题与对应算式连接起来．

    查看答案和解析>>

    同步练习册答案