
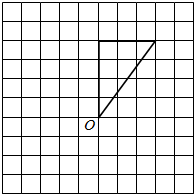
 画出正确的图形
画出正确的图形分析 (1)根据旋转的特征,三角形绕点O顺时针旋转90°,点O的位置不动,其余各部分均绕此点按相同相同方向旋转相同的度数即可画出旋转后的图形.
(2)根据轴对称图形的特征,对称点到对称轴的距离相等,对称点的连线垂直于对称轴,以点O所在纵向直线为对称,在对称轴的左边画出(1)图的关键对称点,依次连结即可.
(3)根据三角形面积计算公式“S=$\frac{1}{2}$ah”即可求出(2)中的图形面积.
解答 解:(1)将图形绕O点顺时针旋转90°(下图):
(2)将(1)中所得的图形画出另一半,使它成为一个轴对称图形(下图):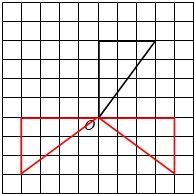
(3)4×2×$\frac{1}{2}$×2
=8×$\frac{1}{2}$×2
=4×2
=8
答:(2)中的图形面积是8.
点评 此题主要是考查作旋转一定度数后的图形、作轴对称图形、三角形面积的计算.


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案科目:小学数学 来源: 题型:填空题
| 150分<3时 | 1千米>999米 | 50厘米<45分米 |
| $\frac{3}{5}$<$\frac{4}{5}$ | $\frac{1}{6}$>$\frac{1}{8}$ | 5千克=5000克 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com