分析:连接A
1C,
,
因为三角形A
1BC与三角形ABC的底相等,A
1D=(1-
)AD,所以三角形A
1BC的面积是三角形ABC面积的(1-
);
又因为三角形A
1B
1C与三角形A
1BC的高相等,A
1B
1=
A
1B,所以三角形A
1B
1C的面积是三角形A
1BC面积的
;
又因为三角形A
1B
1C
1与三角形A
1B
1C底相等,B
1C
1=
B
1C,所以三角形A
1B
1C
1的面积是三角形A
1B
1C的面积的
.
所以三角形A
1B
1C
1的面积=1×
×
×
=
.据此解答即可.
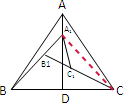
解答:解:如图所示:

,连接A
1C,
因为三角形A
1BC与三角形ABC的底相等,A
1D=(1-
)AD,所以三角形A
1BC的面积=三角形ABC面积×(1-
)=1×
=
;
因为三角形A
1B
1C与三角形A
1BC的高相等,A
1B
1=
A
1B,所以三角形A
1B
1C的面积=三角形A
1BC面积的
=
×=
;
因为三角形A
1B
1C
1与三角形A
1B
1C底相等,B
1C
1=
B
1C,所以三角形A
1B
1C
1的面积=三角形A
1B
1C的面积的
=
×=
.
答:三角形A
1B
1C
1的面积是
.
点评:解决本题的关键是根据如果两个三角形的底相等,则面积之比等于高之比;如果两个三角形的高相等,那么面积之比等于两个三角形的底之比.

 如图,在三角形ABC中,BD=DC,AA1=
如图,在三角形ABC中,BD=DC,AA1= ,
, ,连接A1C,
,连接A1C,

 备战中考寒假系列答案
备战中考寒假系列答案