
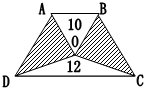
 如图,在梯形ABCD内有两个三角形的面积分别是10与12,已知梯形的上底AB的长是下底DC的长的$\frac{2}{3}$,那么余下的阴影部分的面积是多少?
如图,在梯形ABCD内有两个三角形的面积分别是10与12,已知梯形的上底AB的长是下底DC的长的$\frac{2}{3}$,那么余下的阴影部分的面积是多少? 分析 根据题意和图形可知:已知的2个三角形高的和是梯形的高,2个三角形底的和是梯形上下底的和.而梯形和三角形的面积都和底高有关系,所以设出其中一个三角形的底和高,可以变相求出梯形的面积,再减去已知的2个三角形的面积就可以求出阴影的面积.
解答 解:设上底长为2a,下底长为3a,三角形AOD的高为h,则三角形BCO的高为x,则x是:
(2a×h):(3a×x)=10:12 解之得:x=$\frac{4}{5}$h
那么梯形的高为:h+$\frac{4}{5}$h=$\frac{9}{5}$h
又因为三角形AOD面积为10,可知:ah=10
梯形面积为:(2a+3a)×$\frac{9}{5}$h÷2=$\frac{9}{2}$ah=$\frac{9}{2}$×10=45
故阴影面积为:45-(10+12)=23
答:阴影部分的面积是23.
点评 本题图形提示阴影的面积=梯形的面积-2个已知三角形的面积,还是运用组合图形面积求法的思想.


科目:小学数学 来源: 题型:解答题
查看答案和解析>>
科目:小学数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com