
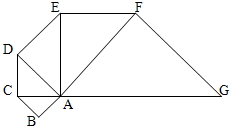
 如图,以等腰直角三角形ABC的斜边AC为直角边,画第二个等腰直角三角形ACD,再以等腰直角三角形ACD的斜边AD为直角边,画第三个等腰直角三角ADE,…,以此类推直到第五个等腰直角三角形AFG.已知,这五个等腰直角三角形的面积和为15.5,求原来等腰直角三角形ABC的直角边的长.
如图,以等腰直角三角形ABC的斜边AC为直角边,画第二个等腰直角三角形ACD,再以等腰直角三角形ACD的斜边AD为直角边,画第三个等腰直角三角ADE,…,以此类推直到第五个等腰直角三角形AFG.已知,这五个等腰直角三角形的面积和为15.5,求原来等腰直角三角形ABC的直角边的长. 分析 假设AB的长为x,那么根据三角形的面积公式可知△ABC的面积就是$\frac{1}{2}$x2;AC2=2x2,等腰直角三角形ACD的面积=$\frac{1}{2}$AC×CD=$\frac{1}{2}$AC2=x2;AD2=2AC2=4x2,等腰直角三角ADE的面积=$\frac{1}{2}$AD×DE=$\frac{1}{2}$AD2=2x2,以此类推,等腰直角三角形AEF的面积=4x2,等腰直角三角形AFG的面积=8x2,根据这五个等腰直角三角形的面积和为15.5列出方程,即可求出原来等腰直角三角形ABC的直角边的长.
解答 解:设AB的长为x,
$\frac{1}{2}$x2+x2+2x2+4x2+8x2=15.5
15.5x2=15.5
x2=1
x=1
或x=-1(不合题意,舍去),
答:原来等腰直角三角形ABC的直角边的长为1.
点评 本题考查了学生对等腰直角三角形和勾股定理的理解和掌握,有一定难度.


科目:小学数学 来源: 题型:填空题

查看答案和解析>>
科目:小学数学 来源: 题型:解答题
查看答案和解析>>
科目:小学数学 来源: 题型:解答题
| $\frac{2}{5}$+$\frac{3}{5}$= | $\frac{5}{6}$-$\frac{1}{4}$= | $\frac{6}{7}$×$\frac{7}{15}$= | $\frac{1}{5}$×$\frac{1}{8}$= |
| $\frac{3}{5}$÷$\frac{1}{3}$= | 0.62= | $\frac{8}{9}$÷4= | 9π= |
| 0÷$\frac{2}{3}$= | $\frac{5}{6}$×30= | 1÷10%= | 0.75+125%= |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com