
| 1 |
| 3 |
| 1 |
| 4 |


 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:小学数学 来源: 题型:
 如图是华联商厦3月份甲,乙,丙三种品牌彩电的销售量统计图,预测4月份甲,乙,丙三种品牌彩电的销售量将分别增长5%,10%和20%.根据预测,甲,丙两种品牌彩电4月份的销量之和为
如图是华联商厦3月份甲,乙,丙三种品牌彩电的销售量统计图,预测4月份甲,乙,丙三种品牌彩电的销售量将分别增长5%,10%和20%.根据预测,甲,丙两种品牌彩电4月份的销量之和为查看答案和解析>>
科目:小学数学 来源: 题型:
| 1 |
| 2 |
| 2 |
| 3 |
查看答案和解析>>
科目:小学数学 来源: 题型:
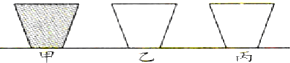 如图,甲、乙、丙三个大小相同的杯子在桌面上一次排列,其中甲杯中盛满水,乙和丙是空杯.现把水全部倒入相邻(左或右)的空杯中,那么,经过55次倒水后,有水的是
如图,甲、乙、丙三个大小相同的杯子在桌面上一次排列,其中甲杯中盛满水,乙和丙是空杯.现把水全部倒入相邻(左或右)的空杯中,那么,经过55次倒水后,有水的是查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com