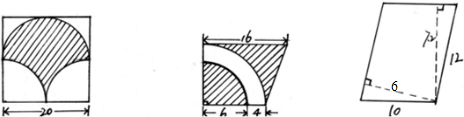
分析:(1)根据题干,上部的两处空白处的面积等于正方形的面积减去正方形内最大的圆的面积的差的一半,据此可得阴影部分的面积等于正方形的面积减去两处空白处的面积,再减去这直径是20的半圆的面积;
(2)观察图形可知,阴影部分的面积等于图形中梯形的面积减去外圆半径是6+4=10,内圆半径是6的
圆环的面积,据此利用公式计算即可;
(3)此题是求平行四边形的面积,找准一组对应的底与高的值,利用平行四边形的面积公式计算即可解答.
解答:解:(1)上部的两处空白处的面积是:[20×20-3.14×
()2]÷2,
=[400-314]÷2,
=86÷2,
=43,
所以阴影部分的面积是:20×20-43-3.14×
()2÷2,
=357-157,
=300,
答:阴影部分的面积是300.
(2)6+4=10,
(10+16)×10÷2-
×3.14×(10
2-6
2),
=130-50.24,
=79.76,
答:阴影部分的面积是79.76.
(3)10×7.2=72,
答:这个平行四边形的面积是72.
点评:此题主要考查组合图形的面积的计算方法,利用面积转化是解决此类问题的关键.



 阅读快车系列答案
阅读快车系列答案