需要3根小棒，摆
需要5根小棒，…，像这样摆n个三角形需要2n+1根小棒；当n=50时，需要101根小棒． 分析 摆一个三角形需要3根小棒，摆两个三角形需要5根小棒，摆三个三角形需要7根小棒，每增加一个三角形就增加2根小棒，则知摆n个三角形需要（2n+1）根小棒，据此算出n=50时即可解答问题．
解答 解：由分析及规律知：摆n个三角形需要（2n+1）根小棒，n为正整数，
当n=50时，
2n+1
=2×50+1
=101（根），
答：像这样摆n个三角形需要 2n+1根小棒；当n=50时，需要 101根小棒．
故答案为：2n+1；101．
点评 本题是一道找规律的题目，这类题型在考试中经常出现．对于找规律的题目首先应找出哪些部分发生了变化，是按照什么规律变化的．
科目：小学数学 来源： 题型：填空题
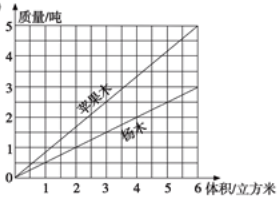看图回答问题．如图是材料加工场李叔叔绘制的杨木和苹果木的体积与质量变化规律图．查看答案和解析>>
科目：小学数学 来源： 题型：计算题
| 600-298= | 3.2+6.8= | 5÷2.5= | 42= |
| 4.5×0.8= | $\frac{1}{2}$-$\frac{1}{3}$= | $\frac{7}{11}$×$\frac{11}{7}$= | 1+$\frac{4}{5}$÷$\frac{4}{5}$= |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
