Question

下面的图形中，图（　　）的面积最小．

A．1

B．2

C．3

Answer 1

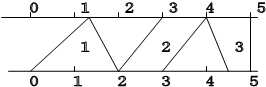
分析：根据三角形的面积=

1

2

×底×高，平行四边形的面积=底×高，梯形的面积=

1

2

×（上底+下底）×高；由图可知，梯形、三角形、平行四边形的高相等，分别求得它们的面积进而比较即可．

解答：解：因为它们的高相等，假设是h，三角形的底是2，面积=2×h÷2=1h；平行四边形的底是1，面积=1×h=1h；梯形的上底是1、下底是0.5，面积=（0.5+1）×h÷2=0.75h；
1h＞0.75h；
所以，图3梯形的面积最小；
故选：C．

点评：此题主要根据平行线的性质，得出梯形、三角形、平行四边形的高相等，求出三角形、梯形与平行四边形的面积进行比较，由此解决问题．