练习册

  • 练习册
  • 试题
    精英家教网 > 小学数学 > 题目详情
    由6、7、8、9组成的各位数字互不相同的四位数中，能被11整除的数有
    8
    8
    个．
    分析：能被11整除数的特征是：奇数数位的数字之和减去偶数数位数字之和，所得差能被11整除，这个数就能被11整除，因此6、9如果在千位、十位，则7、8在百位、个位，反之也可，由此写出结果即可．
    解答：解：6在千位，9在十位，能被11整除的数有6798，6897；
    9在千位，6在十位，能被11整除的数有9768，9867；
    8在千位，7在十位，能被11整除的数有8976，8679；
    7在千位，8在十位，能被11整除的数有7986，7689；
    综上所知，能被11整除的数有8个．
    故答案为：8．
    点评：此题主要利用被11整除的特征：奇数数位的数字之和减去偶数数位数字之和，所得差能被11整除，这个数就能被11整除解答此题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：小学数学 来源： 题型：

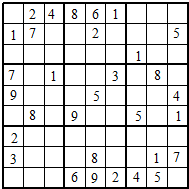    9、“九宫阵”是一个9×9的方阵，它是由九个3×3的“九宫格”（图中黑实线围住的方阵）组成．请你在下图中将数字1，2，3，4，5，6，7，8，9分别填入空格内，使得每行、每列及9个“九宫格”中数字1～9均恰好出现一次．当填写完后，那么，位于第4行第4列的数字是（　　）

    查看答案和解析>>

    科目：小学数学 来源： 题型：

    由1、2、3、4、5、6、7、8、9这9个数字组成的九位数可以是质数吗？

    查看答案和解析>>

    科目：小学数学 来源： 题型：

    由数字1、2、3、4、5、6、7、8、9组成一切可能的没有重复数字的四位数，这些四位数之和是
    16798320
    16798320
    ．

    查看答案和解析>>

    科目：小学数学 来源： 题型：

    王老师在黑板上写了这样的乘法算式：12345679×
    72
    72
    =□□□□□□□□□，然后说道：“只要同学们告诉我你喜欢1，2，3，4，5，6，7，8，9中的哪个数，我在括号里填上适当的乘数，右边的积一定全由你喜欢的数字组成．”小明抢着说：“我喜欢3．”王老师填上乘数“27”，结果积就出现九个3：
    12345679×（27）=333333333
    小宇说：“我喜欢7．”只见王老师填上乘数“63”，积就出现九个7：
    12345679×（63）=777777777
    小丽说：“我喜欢8．”那么算式中应填上的乘数是
    72
    72
    ．

    查看答案和解析>>

    同步练习册答案