Question

已知S_△DOC=15平方厘米，BO=

2

3

BD．求梯形的面积．

Answer 1

分析：由BO=

2

3

BD推出OD=

1

2

OB，S△BCO=2S△DOC，算出△DBC=45平方厘米，由AD∥BC推出AD=

1

2

BC，又因△DBC与梯形ABCD等高，可根据三角形和梯形的面积公式进行等量代换，推算出梯形的面积．

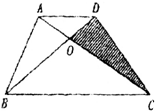
解答：解：设梯形的高为h，它也是△DBC的高，
因为OB=

2

3

BD，BD=BO+OD，
所以BO=2OD，
又因为在△AOD和△DBC里，AD∥BC，BO=2OD，
所以AD=

1

2

BC
因为△DOC与△BOC等高，BO=2OD，S△DOC=15平方厘米，
所以S△BOC=2△DOC=2×15=30（平方厘米），
因为S△DBC=S△DOC+S△BOC，
所以S△DBC=15+30=45（平方厘米），
又因为S△DBC=

1

2

×BC×h，
所以

1

2

BCh=45，
因为梯形ABCD的面积=

1

2

（AD+BC）h，
所以梯形ABCD的面积=

1

2

（

1

2

BC+BC）h，
=

3

2

×

1

2

BCh，
=

3

2

×45，
=67.5（平方厘米），
答：梯形的面积是67.5平方厘米．

点评：此题主要是根据B0=2OD，找出AD与BC、梯形ABCD与三角形BDC的关系．