
 如图所示,一个圆周上有9个位置,依次编为1~9号.现在有一个小球在1号位置上,第一天顺时针前进10个位置,第二天逆时针前进14个位置.以后,第奇数天与第一天相同,顺时针前进10个位置,第偶数天与第二天相同,逆时针前进14个位置.问:至少经过多少天,小球又回到1号位置.
如图所示,一个圆周上有9个位置,依次编为1~9号.现在有一个小球在1号位置上,第一天顺时针前进10个位置,第二天逆时针前进14个位置.以后,第奇数天与第一天相同,顺时针前进10个位置,第偶数天与第二天相同,逆时针前进14个位置.问:至少经过多少天,小球又回到1号位置.

科目:小学数学 来源: 题型:
 如图所示,在一个圆周上放了1枚黑色的围棋子和2012枚白色的围棋子.若从黑子开始,按顺时针方向,每隔1枚,取走1枚,则当取到黑子时,圆周上还剩下
如图所示,在一个圆周上放了1枚黑色的围棋子和2012枚白色的围棋子.若从黑子开始,按顺时针方向,每隔1枚,取走1枚,则当取到黑子时,圆周上还剩下查看答案和解析>>
科目:小学数学 来源: 题型:
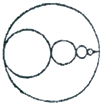 有一个大圆,如果以他的一个直径上的无数个点为圆心,划出无数个紧密相连的小圆(如图所示).大圆周长与大圆内这些无数小圆周长之和相比较,谁更长一些?为什么?
有一个大圆,如果以他的一个直径上的无数个点为圆心,划出无数个紧密相连的小圆(如图所示).大圆周长与大圆内这些无数小圆周长之和相比较,谁更长一些?为什么?查看答案和解析>>
科目:小学数学 来源: 题型:解答题
 有一个大圆,如果以他的一个直径上的无数个点为圆心,划出无数个紧密相连的小圆(如图所示).大圆周长与大圆内这些无数小圆周长之和相比较,谁更长一些?为什么?
有一个大圆,如果以他的一个直径上的无数个点为圆心,划出无数个紧密相连的小圆(如图所示).大圆周长与大圆内这些无数小圆周长之和相比较,谁更长一些?为什么?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com