
分析 把全程的距离看作单位“1”,如果甲车增加全程的$\frac{1}{11}$就和乙车行驶的距离相等了,根据和差公式可得,乙车行驶的距离是(1+$\frac{1}{11}$)÷2=$\frac{6}{11}$,则乙车行驶的距离是1-$\frac{6}{11}$=$\frac{5}{11}$,所以乙甲两车行驶的路程比是$\frac{6}{11}$:$\frac{5}{11}$=6:5,因为时间一定,速度比等于路程比,所以乙车的速度:甲车的速度=6:5,则乙车的速度比甲车的速度快:(6-5)÷5=20%.
解答 解:(1+$\frac{1}{11}$)÷2
=$\frac{12}{11}÷2$
=$\frac{6}{11}$
1-$\frac{6}{11}$=$\frac{5}{11}$
$\frac{6}{11}$:$\frac{5}{11}$=6:5
(6-5)÷5
=1÷5
=20%
答:乙车的速度比甲车的速度快20%.
点评 本题考查了比的应用和相遇问题的综合应用,关键是求出乙甲两车行驶的路程比,即速度比.


科目:小学数学 来源: 题型:操作题
查看答案和解析>>
科目:小学数学 来源: 题型:解答题
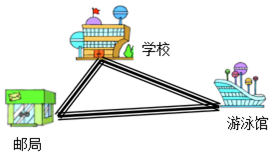 下面是小丁丁的学校到游泳馆、邮局之间的地图.
下面是小丁丁的学校到游泳馆、邮局之间的地图.| 次 | 第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 |
| 10步走的路程(m) | 4.8 | 4.5 | 4.4 | 4.7 | 4.5 | 4.7 |
查看答案和解析>>
科目:小学数学 来源: 题型:解答题
查看答案和解析>>
科目:小学数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com