
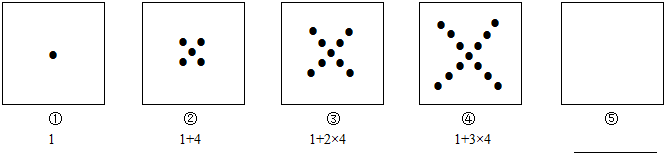
分析 根据第1个方框共有1个点,第2个方框共有1+4(2-1)=5个点,第3个方框共有1+4(3-1)=9个点,第4个方框共有1+4(4-1)=13个点,得出第n个方框共有1+4(n-1)个点,据此解答即可.
解答 解:因为:
第1个方框共有1个点,
第2个方框共有1+4(2-1)=5个点,
第3个方框共有1+4(3-1)=9个点,
第4个方框共有1+4(4-1)=13个点
所以第n个方框共有1+4(n-1)个点,
第⑤个方框有1+4×(5-1)=17个点.
如图:
第8个方框里有1+4×(8-1)=29个点.
第15方框里有1+4×(15-1)=57个点,
第N方框里有1+4(N-1)=4N-3个点,
第100方框里有1+4(100-1)=397个点.
答:第8个方框里有29个点,第15方框里有57个点,第N方框里有4N-3个点,第100方框里有397个点.
故答案为:29,57,4N-3,397.
点评 对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的.


 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:小学数学 来源: 题型:解答题
查看答案和解析>>
科目:小学数学 来源: 题型:解答题
| $\frac{6}{11}$×$\frac{7}{15}$×10 | $\frac{5}{22}$×$\frac{2}{5}$×$\frac{5}{2}$ |
| $\frac{5}{7}$-$\frac{5}{9}$×$\frac{5}{7}$ | 1-$\frac{5}{7}$×$\frac{21}{25}$ |
| $\frac{7}{9}$×($\frac{2}{3}$-$\frac{2}{7}$) | ($\frac{1}{4}$+$\frac{2}{9}$)×3.6 |
| $\frac{4}{7}$×$\frac{5}{9}$+$\frac{3}{7}$×$\frac{5}{9}$ | $\frac{7}{8}$×7+$\frac{3}{8}$. |
查看答案和解析>>
科目:小学数学 来源: 题型:解答题
查看答案和解析>>
科目:小学数学 来源: 题型:选择题
| A. | 甲数>乙数>丙数 | B. | 甲数<乙数<丙数 | C. | 乙数>甲数>丙数 | D. | 甲数>丙数>乙数 |
查看答案和解析>>
科目:小学数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com