
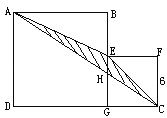
【题目】如图.正方形ABGD与正方形EFGC并放在一起.已知小正方形EFGC的边长是6,求三角形AEC(阴影部分)的面积.
【答案】18
【解析】
试题分析:设大正方形ABCD的边长=a,因为CH∥AD,所以△GHC∽△GAD,所以HC:AD=CG:DG,所以HC:a=6:(6+a),所以HC=6a÷(6+a),EH=EC﹣HC=6﹣6a÷(6+a);三角形AEC(阴影部分)的面积=三角形AEH的面积+三角形GEH的面积=EH×AB÷2+EH×GC÷2=EH×(AB+CG)÷2=[6﹣6a÷(6+a)]×(a+6)÷2=[6×6+6a﹣6a]÷2=6×6÷2=18
解:设大正方形ABCD的边长=a,
因为CH∥AD,
所以△GHC∽△GAD,
所以HC:AD=CG:DG,
所以HC:a=6:(6+a),
所以HC=6a÷(6+a),
EH=EC﹣HC=6﹣6a÷(6+a);三角形AEC(阴影部分)的面积=三角形AEH的面积+三角形GEH的面积,
=EH×AB÷2+EH×GC÷2=EH×(AB+CG)÷2,
=[6﹣6a÷(6+a)]×(a+6)÷2,
=[6×6+6a﹣6a]÷2,
=6×6÷2,
=18;
答:三角形AEC(阴影部分)的面积是18.


 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:小学数学 来源: 题型:
【题目】如图,正方形网格中,△ABC是格点三角形,将△ABC绕点A按逆时针方向旋转90゜得到△AB1C1.
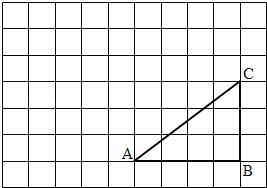
(1)在正方形网格中,作出△AB1C1;
(2)设每个网格小正方形的边长是1cm,用阴影部分表示出旋转过程中线段BC所扫过的面积,然后求出它的面积.(π取3)
查看答案和解析>>
科目:小学数学 来源: 题型:
【题目】学校食堂有一个底面直径是60厘米,高80厘米的圆柱形水箱,水箱中装有A、B两个进水管,先开A管,过一段时间后两管同开,下面折线图表示进水情况,请根据图回答以下问题.
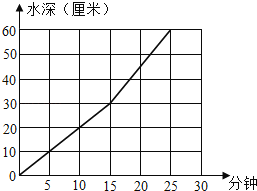
(1)A管开放多少分钟后,B管开始与A管同时进水?
(2)A管12分钟进水多少升?
(3)A、B两管同时进水,每分钟进水多少升?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com