
分析 根据顺水速=静水速+水流速度,设船在静水中的速度为x,原来的水速为y,根据甲港到乙港顺流航行需1小时可得总路程是(x+y),水流增加倍后总路程=$\frac{5}{6}$(x+2y);从乙港返回甲港是逆流航行时间=总路程÷(x-2y),根据总路程不变即可得出乙港返回甲港时间.据此解答.
解答 解:设船在静水中的速度为x,原来的水速为y,根据题意得:
50分钟=$\frac{5}{6}$小时
甲港到乙港两次路程相等得
x+y=$\frac{5}{6}$(x+2y)
6x+6y=5x+10y
x=4y;
水流速度增加后,从乙港返回甲港需航行时间
x+y÷(x-2y)
=(4y+y)÷(4y-2y)
=5y÷2y
=2.5(小时).
答:从乙港返回甲港需航行2.5小时.
故答案为:2.5.
点评 本题考查了流水行船问题,关键是根据水流增加后,走的路程不变,求出静水速与水流速度的关系.


科目:小学数学 来源: 题型:填空题
| 11×11=121 | 12×11=132 | 13×11=143 | 14×11=154 |
| 15×11=165 | 16×11=176 | 43×11=473 | 68×11=748 |
查看答案和解析>>
科目:小学数学 来源: 题型:选择题
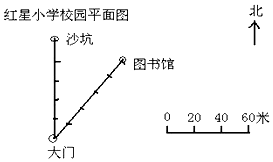
| A. | 沙坑位于大门的正北方向100米处 | |
| B. | 图书馆位于大门北偏西方向100米处 | |
| C. | 图书馆位于大门北偏东方向100米处 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com