Question

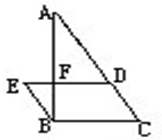
如图，AF=3FB，FD=3EF，直角三角形ABC的面积是48平方厘米．求平行四边形EBCD和三角形AFD的面积．

Answer 1

分析：由题意知三角形ABC的面积，又是直角三角形，所以

1

2

×AB×BC=48，要求平行四边形的面积就用BC×BF又因AF=3FB，FD=3EF，可知AB=AF+BF=4BF，ED=EF+DF=4EF；找到与三角形的关系求出面积，根据三角形的面积公式可得三角形AFD的面积=

1

2

×DF×AF，由平行四边行可知

DF

BC

=

AF

AB

=

3BF

4BF

=

3

4

再找到与三角形ABC的关系从而算出的面积．

解答：解：由平行四边形特点可知：DE∥BC，
所以：

DF

BC

=

AF

AB

=

3BF

4BF

=

3

4

，
设，平行四边形的面积为X厘米²，S_△ABC=48

S△ABC

S平行四边形

=

AB×BC÷2

BC×BF

=

AB÷2

BF

=2，

48

X

=2，
X=24，
S_△AFD=AF×DF÷2，S_△ABC=AB×BC÷2，

AF

AB

=

3

4

，

DF

BC

=

3

4

，S_△ABC=48厘米²，设S_△AFD为y，列出比例

S△AFD

S△ABC

=

AF×DF÷2

AB×BC÷2

=

3

4

×

3

4

=

9

16

，

y

48

=

9

16

，
16y=48×9，
y=48×9÷16，
y=27，
答：平行四边形EBCD和三角形AFD的面积各是24平方厘米，27平方厘米．

点评：此题重在根据三角形和平行四边形的面积公式，及题中条件找出等量关系式再利用比例知识完成此题．