
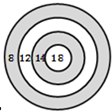
 某次射箭比赛中,所用的箭靶上画有4个同心圆环,从外到内,分别标上8、12、14、18,如图,每个圆环内的数是射中此圆环时可得到的分数.运动员林得胜射中10支箭,每个圆环都有箭射中,共得110分.问:每个圆环各被射中几支箭?(在下面写出所有可能出现的情况的答案,分析过程可不写.)
某次射箭比赛中,所用的箭靶上画有4个同心圆环,从外到内,分别标上8、12、14、18,如图,每个圆环内的数是射中此圆环时可得到的分数.运动员林得胜射中10支箭,每个圆环都有箭射中,共得110分.问:每个圆环各被射中几支箭?(在下面写出所有可能出现的情况的答案,分析过程可不写.)| (8分)环 | (12分)环 | (14分)环 | (18分)环 | |
| 第1种情况各环射中支数 | 6 | 1 | 1 | 2 |
| 第2种情况各环射中支数 | 5 | 2 | 2 | 1 |


 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:小学数学 来源: 题型:
 某次射箭比赛中,所用的箭靶上画有4个同圆心的圆环.如图,每个圆环内的数字是射中此圆环时可得到的分数,运动员黄亮射中10支箭,每个圆环都有箭射中,共得110分,问:每个圆环各被射中几支?
某次射箭比赛中,所用的箭靶上画有4个同圆心的圆环.如图,每个圆环内的数字是射中此圆环时可得到的分数,运动员黄亮射中10支箭,每个圆环都有箭射中,共得110分,问:每个圆环各被射中几支?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com