
分析 对于此数列的每一个数,都可以写成1+3+3+…+3的形式,根据被3整除的特征,加以判断.
解答 解:对于此数列的每一个数,都可以写成1+3+3+…+3的形式,若这个数为第n项,那么1+3+3+…+3中就有(n-1)个3,
如果一个数是3的倍数,那么将它拆分,一定能拆为若干个3的和,
显然,这个数列里每个数都是1+3+3+…+3的形式,不能写成若干个3的和,
所以这个数列里的每一项都不是3的倍数.
故答案为:√.
点评 此题主要考查了被3整除的数的特征.


科目:小学数学 来源: 题型:计算题
| 4.8×99+4.8 | 75×24+836÷4 | 12$\frac{9}{11}$-($\frac{9}{11}$+$\frac{5}{13}$) |
| 200.9×73-6.3×2009 | $\frac{3}{5}$($\frac{1}{7}$+$\frac{8}{21}$÷$\frac{2}{3}$) | $\frac{1}{6}$÷[1÷($\frac{3}{5}$-$\frac{3}{10}$)]. |
查看答案和解析>>
科目:小学数学 来源: 题型:操作题
 如图所示:
如图所示:查看答案和解析>>
科目:小学数学 来源: 题型:填空题
查看答案和解析>>
科目:小学数学 来源: 题型:填空题
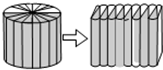 如图所示,把底面直径是8厘米,高是10厘米的圆柱切成若干等分,拼成一个近似的长方体,这个近似长方体的长是12.56厘米,宽是4厘米,高是10厘米,体积是502.4立方厘米.
如图所示,把底面直径是8厘米,高是10厘米的圆柱切成若干等分,拼成一个近似的长方体,这个近似长方体的长是12.56厘米,宽是4厘米,高是10厘米,体积是502.4立方厘米.查看答案和解析>>
科目:小学数学 来源: 题型:应用题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com