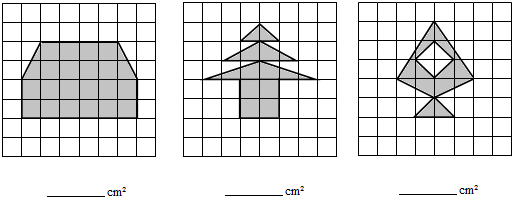
考点:组合图形的面积
专题:平面图形的认识与计算
分析:(1)此图可以分成上面一个梯形和下面的一个长方形,利用梯形与长方形的面积公式计算即可解答问题;
(2)此图上面是3个三角形、下面是一个正方形,据此利用三角形和正方形的面积公式计算即可解答问题;
(3)此图可以分成3部分:上、中、下各一个三角形,再减去空白处的边长是1厘米的四个直角三角形的面积即可解答问题.
解答:
解:(4+6)×2÷2+6×2
=10+12
=22(平方厘米)
答:这个图形的面积是22平方厘米.
(2)2×1÷2+4×1÷2+6×1÷2+2×2
=1+2+3+4
=10(平方厘米)
答:这个图形的面积是10平方厘米.
(3)4×3÷2+4×1÷2+2×1÷2-1×1÷2×4
=6+2+1-2
=7(平方厘米)
答:这个图形的面积是7平方厘米.
故答案为:

点评:本题运用梯形的面积公式、长方形的面积公式、三角形的面积公式以及平行四边形的面积公式解答即可.