
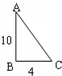
 分别以这个直角三角形的直角边AB、BC为轴旋转一周,都能得到一个圆锥,哪种情况得到的圆锥体积比较大.
分别以这个直角三角形的直角边AB、BC为轴旋转一周,都能得到一个圆锥,哪种情况得到的圆锥体积比较大. πr2h,102×4>42×10,据此即可判断选择.
πr2h,102×4>42×10,据此即可判断选择. πr2h,其余数据相等,变化的是底面半径和高.
πr2h,其余数据相等,变化的是底面半径和高. π×42×10,以BC为轴得到的圆锥的体积是
π×42×10,以BC为轴得到的圆锥的体积是 π×102×4,
π×102×4,

 名师点拨卷系列答案
名师点拨卷系列答案科目:小学数学 来源: 题型:
 数学常识:勾股定理是直角三角形里的一个重要定理.根据勾股定理,在直角三角形中,两条直角边的长度的平方和,等于这个直角三角形斜边长度的平方.例如,假如一个直角三角形的两条直角边的长度分别为a厘米和b厘米,斜边长度为c厘米,则根据勾股定理可得出一条结论:a2+b2=c2.
数学常识:勾股定理是直角三角形里的一个重要定理.根据勾股定理,在直角三角形中,两条直角边的长度的平方和,等于这个直角三角形斜边长度的平方.例如,假如一个直角三角形的两条直角边的长度分别为a厘米和b厘米,斜边长度为c厘米,则根据勾股定理可得出一条结论:a2+b2=c2.查看答案和解析>>
科目:小学数学 来源: 题型:
 如图,直角三角形ABC的三边分别为3cm、4cm、5cm,将这个直角三角形以一条直角边所在的直线为轴旋转一周,求所形成的立体图形的体积(π取近似值3)
如图,直角三角形ABC的三边分别为3cm、4cm、5cm,将这个直角三角形以一条直角边所在的直线为轴旋转一周,求所形成的立体图形的体积(π取近似值3)查看答案和解析>>
科目:小学数学 来源: 题型:解答题
 数学常识:勾股定理是直角三角形里的一个重要定理.根据勾股定理,在直角三角形中,两条直角边的长度的平方和,等于这个直角三角形斜边长度的平方.例如,假如一个直角三角形的两条直角边的长度分别为a厘米和b厘米,斜边长度为c厘米,则根据勾股定理可得出一条结论:a2+b2=c2.
数学常识:勾股定理是直角三角形里的一个重要定理.根据勾股定理,在直角三角形中,两条直角边的长度的平方和,等于这个直角三角形斜边长度的平方.例如,假如一个直角三角形的两条直角边的长度分别为a厘米和b厘米,斜边长度为c厘米,则根据勾股定理可得出一条结论:a2+b2=c2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com