考点:组合图形的计数
专题:几何的计算与计数专题
分析:(1)根据线段上有5个点,得出线段的条数为10条,从而得出矩形的个数;
(2)根据矩形各条边的长度表示出各个矩形的面积,进而得出总的面积之和.
解答:
解:(1)图中长的一边有5个分点(包括端点),所以长的一边上不同的线段共有1+2+3+4=10(条).
同样,宽的一边上不同的线段也有10条.
所以共有长方形10×10=100(个).
答:图中一共有100个长方形.
(2)因为长的一边上的10条线段长分别为5,17,25,26,12,20,21,8,9,1,
宽的一边上的10条线段长分别为2,6,13,16,4,11,14,7,10,3.
所以所有长方形面积和
(5×2+5×6+…+5×3)+(17×2+17×6+…+17×3)+…+(1×2+1×6+…+1×3)
=(5+17+…+1)×(2+6+…+3)
=144×86
=12384.
答:所有这些长方形的面积和是12384.
点评:此题主要考查了矩形的面积求法以及线段条数的数法,利用点分成线段条数得出矩形个数,从而求出矩形面积题目有一定抽象性,应认真分析,从而确定解题思路.

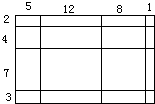 (1)图中一共有多少个长方形?
(1)图中一共有多少个长方形?
