
分析 削去的体积=圆柱的体积-长方体的体积,根据题干分析可得,削出的这个长方体的高是h,底面积是圆柱的底面圆的内接正方形,这个正方形的面积=圆柱的底面直径×半径,即2a2,由此利用圆柱和长方体的体积公式即可求出削去的体积,最后除以原来圆柱体的体积即可.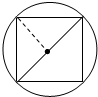
解答 解:3×a2×h-2a×a×h
=3a2h-2a2h
=a2h
a2h÷(3×a2×h)
=a2h÷3a2h
=$\frac{1}{3}$
答:削去了原来的$\frac{1}{3}$.
故答案为:$\frac{1}{3}$.
点评 此题考查圆柱和长方体的体积公式的灵活应用,关键是根据圆内接正方形的特点求出长方体的底面积.


 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案科目:小学数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com