
科目: 来源:数学教研室 题型:072
如图所示赛场地,在
400米比赛时,第三条跑道的起跑线画在第一条跑道起跑线的前面。已知每条跑道宽1.5米,那么第三条跑道线应该画在第一条跑道线前面多少米?
查看答案和解析>>
科目: 来源:数学教研室 题型:072
如下图,
6名运动员在运动场上进行200米赛跑,每条跑道宽约为1.2米。弯道部分为半圆,最内圈的弯道半径约为31.7米。(结果用π表示)
(1)最内圈弯道全长为________米。
(2)靠内第二圈弯道半径为________米,这个弯道全长为________米。
(3)相邻两跑道弯道部分相差________米。
(4)第六道起跑线与第一道应相差________米。
查看答案和解析>>
科目: 来源:数学教研室 题型:072
世界杯足球赛上的数学问题
韩日世界杯的硝烟已散去,但“世界杯”却是永恒的话题,也许你是一个球迷,不知你想过没有,其实世界杯也与许多有趣的数学问题相关。下面我们讨论两个问题,在世界杯小组赛上每四个队进行单循环比赛,每场比赛胜队得
3分,负队得0分,平局两队各得1分。小组赛结束后,总积分最高的两个队出线,进入下一轮比赛,如果总积分相同,还要按下一步的规则排序。提问一 一支队为了晋级,下一轮至少要积几分才能保证必然出线
?为什么?讨论:
4个队单循环要赛六场,每场比赛最多产生3分,6场比赛最多产生18分。(1)若某队积6分,则剩下12分,可能有另两队也各得6分,这样就要按进一步规则排序,因此该队有可能不出线。
(2)若一个队积7分,则最多剩下11分,这样另三个队中不可能再有两个队积分等于或者超过7分,这样该队必然出线。
结论:因此为了晋级下一轮,至少要积
7分。提问二 一队只积
3分,这个队有可能出线吗?为什么?讨论:第一种情况是
6场比赛都是平局,4个队都只得了3分,按进一步规则顺序,该队如果处于前两位,就有可能出线。还有一种情况该队也可能出线,前提是该队也是平
3场,大家能想出来吗?下图是比赛的一种结果。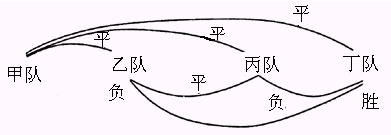
甲队得
3分,乙队得1分,丙队得1分,丁队得7分,则甲队居第二必出线。思考: 一个球队积
2分能出线吗?查看答案和解析>>
科目: 来源:数学教研室 题型:072
小强的卧室如图所示,左、右两个墙上分别有一扇门和一扇窗户,窗户宽为
1.5米,高为1米,门高为2米,宽为0.8米。
(1)
左、右两个墙面(除去窗户和门)的面积分别为________ 和________
和________ 。
。
(2)
如果想粉刷房间里除地面以外的五个墙面,那么需粉刷的墙的面积共为________ 。
。
(3)
按照经验,第一遍粉刷时,每平方米需用涂料约0.5升,那么小强的卧室在第一遍粉刷时共需涂料________升,在第二遍粉刷时,每平方米所需涂料是第一遍的 ,那么第二遍时约需涂料________升,刷两遍共用涂料约________升。
,那么第二遍时约需涂料________升,刷两遍共用涂料约________升。查看答案和解析>>
科目: 来源:数学教研室 题型:072
有
A、B、C、D、E、F六个孩子。已知:(1)B比A高11厘米;(2)C比D矮1厘米;(3)E比B高2厘米;(4)F比B矮7厘米,比D矮2厘米;(5)六人中最矮的身高159厘米。那么,最高的孩子是谁?身高几厘米?E和C的身高相差几厘米?根据条件,你能排出他们的高矮顺序及他们分别相差多少厘米吗?
查看答案和解析>>
科目: 来源:数学教研室 题型:072
分发飞机票三位旅客阿亮、阿玲和阿美同时到售票处预定广州、上海、杭州三地的飞机票,待机票办好之后,售票员分发机票时,问他们分别要哪一张,阿亮说:“我不要广州的。”阿玲说:“我不要上海的。”阿美说:“我不要杭州的,也不要上海的。”请帮助售票员分发一下飞机票,可以尝试从不同角度通过列表方式加以解决。

查看答案和解析>>
科目: 来源:数学教研室 题型:072
(1)
工人师傅利用边角余料铺地板时,用六个形状一样的三角形拼在一起,能够无缝隙地覆盖住A点及其周围小区域,用四个形状一样的四边形拼在一起,也能无缝隙地盖住A点及其周围小区域,从上述的两种覆盖中,我们发现:要完全盖住A点及其周围小区域,必须满足的条件是:拼在A处并以A为顶点的几个角的度数和为________。用边长相等、各角相等的正五边形不能覆盖住A点及其周围小区域的理由是:________之和小于360°,而________之和________360°。(2)
有边数分别为x、y、z,型号不同的多边形,且每种型号的多边形均满足各边相等、各角相等;如果每种型号的多边形各取一个,拼在A点,恰好能覆盖住A点及其周围小区域,请你提出一个关于x、y、z之间关系的猜想,并加以证明。查看答案和解析>>
科目: 来源:数学教研室 题型:072
议一议
(1)
正六边形能否密铺?简述你的理由。(2)
分析图,讨论正五边形不能密铺的原因。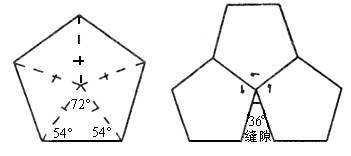
(3)
还能找到能密铺的其他正多边形吗?通过上述问题的探讨研究,可以看出对于给定的某种正多边形,它能否拼成一个平面图形,既不留下一丝空白,又不相互重叠,显然与它的内角大小有关。为了探索哪些正多边形能铺满平面,请根据图,用计算器或量角器完成下表:

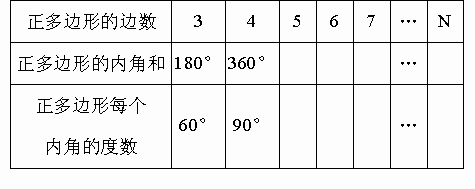
通过上面研讨和计算,我们可以发现:当围绕一点拼在一起的几个多边形的内角加在一起恰好组成一个周角时,就拼成一个平面图形。
如正六边形的每个内角为
120°,三个120°拼在一起恰好组成周角,所以全用正六边形瓷砖就可以铺满地面。所以用相同的正多边形拼地板或用两种以上的正多边形拼地板都可以达到密铺的目的,甚至一些不规则的图形也可以做到,如图所示。
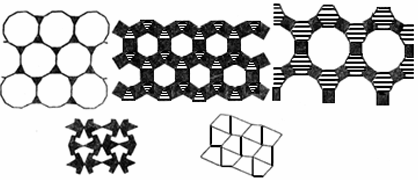
通过这节的学习,你学到了哪些知识,有哪些收获,能否运用你所学过的知识试着完成下列问题。
查看答案和解析>>
科目: 来源:数学教研室 题型:072
李小峰在“改造哈尔滨旧房屋”活动中,分到一套新楼房,准备用地砖密铺新居地面。要求地砖都是正多边形,每块地砖的各边长都相等,各个角也相等,某家装饰市场有如下五种型号的地砖,它们每个角的度数分别是
60°、90°、108°、120°、135°,这些地板砖哪些适用?哪些不适用?说说你的理由。查看答案和解析>>
科目: 来源:数学教研室 题型:072
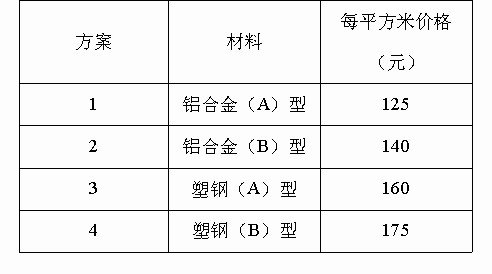
陈红家最近买了一套二手房,窗户总面积是
36平方米。他们家打算用6000元钱把原来的钢窗换成流行的塑钢窗或铝合金窗。目前,市场上这两种材料的价格如下表:请你帮助算一算,选用其中的哪一种方案,才不会超出预算,安装完还能剩下多少钱
?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com