
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,抛物线经过
,抛物线经过![]() 、
、![]() 、
、![]() 三点,连接
三点,连接![]() 、
、![]() 、
、![]() ,线段
,线段![]() 交
交![]() 轴于点
轴于点![]() ,已知实数
,已知实数![]() 、
、![]()
![]() 分别是方程
分别是方程![]() 的两根.
的两根.
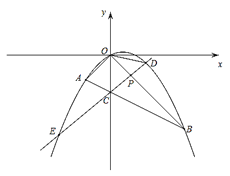
(1)求抛物线的解析式;
(2)若点![]() 为线段
为线段![]() 上的一个动点(不与点
上的一个动点(不与点![]() 、
、![]() 重合),直线
重合),直线![]() 与抛物线交于
与抛物线交于![]() 、
、![]() 两点(点
两点(点![]() 在
在![]() 轴右侧),连接
轴右侧),连接![]() 、
、![]() .
.
①求![]() 面积的最大值,并写出此时点
面积的最大值,并写出此时点![]() 的坐标;②当
的坐标;②当![]() 为等腰三角形时,请直接写出点
为等腰三角形时,请直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】若一个四边形的一条对角线把四边形分成两个等腰三角形,我们把这条对角线叫这个四边形的和谐线,这个四边形叫做和谐四边形.如菱形就是和谐四边形.

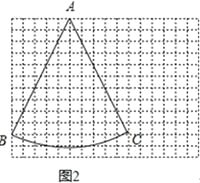
(1)如图1,在梯形ABCD中,AD∥BC,∠BAD=120°,∠C=75°,BD平分∠ABC.求证:BD是梯形ABCD的和谐线;
(2)如图2,在12×16的网格图上(每个小正方形的边长为1)有一个扇形BAC,点A.B.C均在格点上,请在答题卷给出的两个网格图上各找一个点D,使得以A、B、C、D为顶点的四边形的两条对角线都是和谐线,并画出相应的和谐四边形;
(3)四边形ABCD中,AB=AD=BC,∠BAD=90°,AC是四边形ABCD的和谐线,求∠BCD的度数.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() 、
、![]() 两点,点
两点,点![]() 在线段
在线段![]() 上(不含端点
上(不含端点![]() 、
、![]() ).
).

(1)求![]() 、
、![]() 两点的坐标;
两点的坐标;
(2)若![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)若![]() 交直线
交直线![]() 于
于![]() ,
,![]() 于
于![]() ,交
,交![]() 于
于![]() ,
,![]() 为
为![]() 中点,当点
中点,当点![]() 在线段
在线段![]() 上滑动时,求证
上滑动时,求证![]() 的值不变.
的值不变.
查看答案和解析>>
科目: 来源: 题型:
【题目】某商品的进价为每件20元,售价为每件25元时,每天可卖出250件.市场调查反映:如果调整价格,一件商品每涨价1元,每天要少卖出10件.
(1)求出每天所得的销售利润w(元)与每件涨价x(元)之间的函数关系式;
(2)求销售单价为多少元时,该商品每天的销售利润最大;
(3)商场的营销部在调控价格方面,提出了A,B两种营销方案.
方案A:每件商品涨价不超过5元;
方案B:每件商品的利润至少为16元.
请比较哪种方案的最大利润更高,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】为了解某中学学生对“厉行勤俭节约,反对铺张浪费”主题活动的参与情况,小强在全校范围内随机抽取了若干名学生并就某日午饭浪费饭菜情况进行了调查,将调查内容分为四组:![]() 饭和菜全部吃完;
饭和菜全部吃完;![]() :有剩饭但菜吃完;
:有剩饭但菜吃完;![]() :饭吃完但菜有剩;
:饭吃完但菜有剩;![]() :饭和菜都有剩.根据调查结果,绘制了如图所示两幅不完整的统计图.
:饭和菜都有剩.根据调查结果,绘制了如图所示两幅不完整的统计图.

回答下列问题:
(1)这次被抽查的学生共有 人,扇形统计图中,“![]() 组”所对应的圆心角的度数为 ;
组”所对应的圆心角的度数为 ;
(2)补全条形统计图;
(3)已知该中学共有学生![]() 人,请估计这日午饭有剩饭的学生人数,若按平均每人剩
人,请估计这日午饭有剩饭的学生人数,若按平均每人剩![]() 克米饭计算,这日午饭将浪费多少千克米饭?
克米饭计算,这日午饭将浪费多少千克米饭?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知抛物线C1:y=a(x+2)2-5的顶点为P,与x轴相交于A、B两点(点A在点B的左边),点B的横坐标是1.
(1) 求P点坐标及a的值;
(2)如图(1),
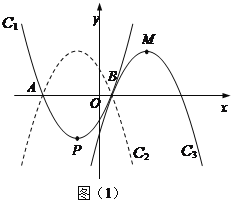
抛物线C2与抛物线C1关于x轴对称,将抛物线C2向右平移,平移后的抛物线记为C3,C3的顶点为M,当点P、M关于点B成中心对称时,求C3的解析式;
(3) 如图(2),
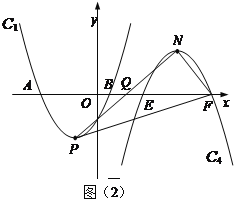
点Q是x轴正半轴上一点,将抛物线C1绕点Q旋转180°后得到抛物线C4.抛物线C4的顶点为N,与x轴相交于E、F两点(点E在点F的左边),当以点P、N、F为顶点的三角形是直角三角形时,求点Q的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知:如图,正方形ABCD,点E是DC边上的一动点,过点C作AE的垂线交AE延长线于点F,过D作DH⊥CF,垂足为H,点O是AC中点,连HO.
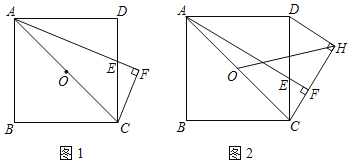
(1)如图1,当∠CAE=∠DAE时,证明:AE=2CF;
(2)如图2,当点E在DC上运动时,线段AF与线段HO之间是否存在确定的数量关系?若存在,证明你发现的结论:若不存在,请说明理由;
(3)当E为DC中点时,AC=2![]() ,直接写出AF的长 .
,直接写出AF的长 .
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,利用一面长为34米的墙,用铁栅栏围成一个矩形自行车场地ABCD,在AB和BC边各有一个2米宽的小门(不用铁栅栏).设矩形ABCD的边AD长为x米,AB长为y米,矩形的面积为S平方米,且x<y.
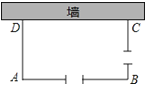
(1)若所用铁栅栏的长为40米,求y与x的函数关系式,并直接写出自变量x的取值范围;
(2)在(1)的条件下,求S与x的函数关系式,并求出怎样围才能使矩形场地的面积为192平方米?
查看答案和解析>>
科目: 来源: 题型:
【题目】要修一个圆形喷水池,在池中心竖直安装一根水管,水管的顶端安一个喷水头,使喷出的抛物线形水柱在与池中心的水平距离为1m处达到最高,高度为3m,水柱落地处离池中心3m,水管应多长?
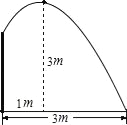
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com