

科目: 来源: 题型:
【题目】某童装专卖店在销售中发现,一款童装每件进价为80元,销售价为120元时,每天可售出20件,为了迎接国庆节,商店决定采取适当的降价措施,以扩大销售量,增加利润,经市场调查发现,如果每件童装降价1元,那么平均可多售出2件.
(1)每件童装降价多少元时,平均每天赢利1200元.
(2)每件童装售价为多少元时,平均每天赢利最大,并求最大利润.
查看答案和解析>>
科目: 来源: 题型:
【题目】杂技团进行杂技表演,演员从跷跷板右端A处弹跳到人梯顶端椅子B处,其身体(看成一点)的路线是抛物线![]() 的一部分,如图
的一部分,如图
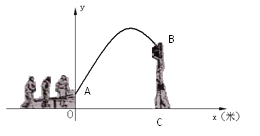
(1)求演员弹跳离地面的最大高度;
(2)已知人梯高BC=3.4米,在一次表演中,人梯到起跳点A的水平距离是4米,问这次表演是否成功?请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】抛物线y=ax2+bx+c的顶点为D(﹣1,2),与x轴的一个交点A在点(﹣3,0)和(﹣2,0)之间,其部分图象如图,则以下结论:①b2﹣4ac<0;②当x>﹣1时,y随x增大而减小;③a+b+c<0;④若方程ax2+bx+c﹣m=0没有实数根,则m>2; ⑤3a+c<0.其中正确结论的个数是( )

A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,若b是正数,直线l:y=b与y轴交于点A;直线a:y=x﹣b与y轴交于点B;抛物线L:y=﹣x2+bx的顶点为C,且L与x轴右交点为D.
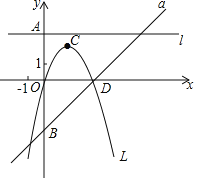
(1)若AB=8,求b的值,并求此时L的对称轴与a的交点坐标;
(2)当点C在l下方时,求点C与l距离的最大值;
(3)设x0≠0,点(x0,y1),(x0,y2),(x0,y3)分别在l,a和L上,且y3是y1,y2的平均数,求点(x0,0)与点D间的距离;
(4)在L和a所围成的封闭图形的边界上,把横、纵坐标都是整数的点称为“美点”,分别直接写出b=2019和b=2019.5时“美点”的个数.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1和2,![]() 中,AB=3,BC=15,
中,AB=3,BC=15,![]() .点
.点![]() 为
为![]() 延长线上一点,过点
延长线上一点,过点![]() 作
作![]() 切
切![]() 于点
于点![]() ,设
,设![]() .
.
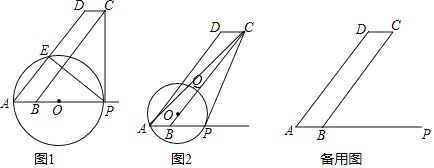
(1)如图1,![]() 为何值时,圆心
为何值时,圆心![]() 落在
落在![]() 上?若此时
上?若此时![]() 交
交![]() 于点
于点![]() ,直接指出PE与BC的位置关系;
,直接指出PE与BC的位置关系;
(2)当![]() 时,如图2,
时,如图2,![]() 与
与![]() 交于点
交于点![]() ,求
,求![]() 的度数,并通过计算比较弦
的度数,并通过计算比较弦![]() 与劣弧
与劣弧![]() 长度的大小;
长度的大小;
(3)当![]() 与线段
与线段![]() 只有一个公共点时,直接写出
只有一个公共点时,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】长为![]() 的春游队伍,以
的春游队伍,以![]() 的速度向东行进,如图1和图2,当队伍排尾行进到位置
的速度向东行进,如图1和图2,当队伍排尾行进到位置![]() 时,在排尾处的甲有一物品要送到排头,送到后立即返回排尾,甲的往返速度均为
时,在排尾处的甲有一物品要送到排头,送到后立即返回排尾,甲的往返速度均为![]() ,当甲返回排尾后,他及队伍均停止行进.设排尾从位置
,当甲返回排尾后,他及队伍均停止行进.设排尾从位置![]() 开始行进的时间为
开始行进的时间为![]() ,排头与
,排头与![]() 的距离为
的距离为![]()
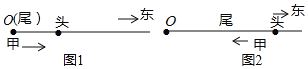
(1)当![]() 时,解答:
时,解答:
①求![]() 与
与![]() 的函数关系式(不写
的函数关系式(不写![]() 的取值范围);
的取值范围);
②当甲赶到排头位置时,求![]() 的值;在甲从排头返回到排尾过程中,设甲与位置
的值;在甲从排头返回到排尾过程中,设甲与位置![]() 的距离为
的距离为![]() ,求
,求![]() 与
与![]() 的函数关系式(不写
的函数关系式(不写![]() 的取值范围)
的取值范围)
(2)设甲这次往返队伍的总时间为![]() ,求
,求![]() 与
与![]() 的函数关系式(不写
的函数关系式(不写![]() 的取值范围),并写出队伍在此过程中行进的路程.
的取值范围),并写出队伍在此过程中行进的路程.
查看答案和解析>>
科目: 来源: 题型:
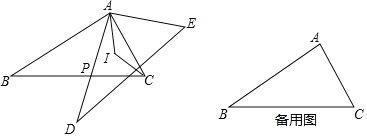
【题目】如图,△ABC和△ADE中,AB=AD=6,BC=DE,∠B=∠D=30°,边AD与边BC交于点P(不与点B,C重合),点B,E在AD异侧,I为△APC的内心.
(1)求证:∠BAD=∠CAE;
(2)设AP=x,请用含x的式子表示PD,并求PD的最大值;
(3)当AB⊥AC时,∠AIC的取值范围为m°<∠AIC<n°,分别直接写出m,n的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某球室有三种品牌的![]() 个乒乓球,价格是7,8,9(单位:元)三种.从中随机拿出一个球,已知
个乒乓球,价格是7,8,9(单位:元)三种.从中随机拿出一个球,已知![]() (一次拿到
(一次拿到![]() 元球)
元球)![]() .
.
(1)求这![]() 个球价格的众数;
个球价格的众数;
(2)若甲组已拿走一个![]() 元球训练,乙组准备从剩余
元球训练,乙组准备从剩余![]() 个球中随机拿一个训练.
个球中随机拿一个训练.
①所剩的![]() 个球价格的中位数与原来
个球价格的中位数与原来![]() 个球价格的中位数是否相同?并简要说明理由;
个球价格的中位数是否相同?并简要说明理由;
②乙组先随机拿出一个球后放回,之后又随机拿一个,用列表法(如图)求乙组两次都拿到8元球的概率.
又拿 先拿 | |||
查看答案和解析>>
科目: 来源: 题型:
【题目】有个填写运算符号的游戏:在“![]() ”中的每个□内,填入
”中的每个□内,填入![]() 中的某一个(可重复使用),然后计算结果.
中的某一个(可重复使用),然后计算结果.
(1)计算:![]() ;
;
(2)若请推算![]() □内的符号;
□内的符号;
(3)在“![]() ”的□内填入符号后,使计算所得数最小,直接写出这个最小数.
”的□内填入符号后,使计算所得数最小,直接写出这个最小数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com