（1）求S与x之间的函数关系式，并写出自变量x的取值范围；

（2）设计费能达到24000元吗？为什么？

（3）当x是多少米时，设计费最多？最多是多少元？

【题目】已知二次函数y＝－x2＋x＋4.

(1)确定抛物线的开口方向、顶点坐标和对称轴；

(2)当x取何值时，y随x的增大而增大？当x取何值时，y随x的增大而减小？

【题目】关于的一元二次方程.

（1）求证：方程总有两个实数根；

（2）若方程有一根小于1，求的取值范围.

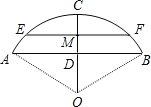
（1）桥拱半径．

（2）若大雨过后，桥下河面宽度（EF）为12米，求水面涨高了多少？

（1）求m的值；

（2）求方程的解.

（1）4（x﹣1）2﹣36＝0（直接开平方法）；

（2）2x2﹣5x+1＝0 （配方法）

（3）（x+1）（x﹣2）＝4（公式法）；

（4）2（x+1）﹣x（x+1）＝0（因式分解法）

解：设所求方程的根为y，则y=2x．所以x=．

把x=代入已知方程，得（）2+﹣3=0，化简，得y2+2y﹣12=0．

故所求方程为y2+2y﹣12=0．

这种利用方程根的代换求新方程的方法，我们称为“换根法”．

问题：已知方程x2+x﹣1=0，求一个一元二次方程，使它的根分别是已知方程根的3倍．

（一）（新知学习）：圆内接四边形的判断定理：如果四边形对角互补，那么这个四边形内接于圆（即如果四边形EFGH的对角互补，那么四边形EFGH的四个顶点E、F、G、H都在同个圆上）．

（二）（问题解决）：已知⊙O的直径为4，AB，CD是⊙O的直径．P是上任意一点，过点P分别作AB，CD的垂线，垂足分别为N，M．

（1）若直径AB⊥CD，点P为上一动点（不与B、C重合）（如图一）．

① 证明：四边形PMON内接于某圆；②证明MN的长为定值，并求其定值；

（2）若直径AB与CD相交成120°角．

① 当点P运动到的中点时（如图二），求MN的长；

② 当点P（不与B、C重合）从B运动到C的过程中（如图三），证明MN的长为定值．

（3）试问当直径AB与CD相交角∠BOC=______度时，MN的长取最大值，其最大值为_____．

【题目】如图，AB是⊙O的直径，点C为⊙O上一点，点P是半径OB上一动点（不与O，B重合），过点P作射线l⊥AB，分别交弦BC，于D、E两点，在射线l上取点F，使FC＝FD．

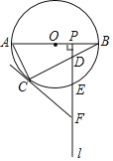
（1）求证：FC是⊙O的切线；

（2）当点E是的中点时，

① 若∠BAC＝60°，判断以O，B，E，C为顶点的四边形是什么特殊四边形，并说明理由；

② 若，且AB＝20，求OP的长．

(1) 求证：A、E、C、F四点共圆；

(2) 设线段 BD与(1)中的圆交于M、N．求证：BM = ND