
科目: 来源: 题型:
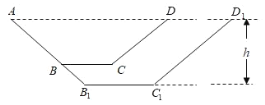
【题目】某农场灌溉水渠长为1000米,横截面是等腰梯形,如图,在等腰梯形![]() 中,
中,![]() ,
,![]() ,其中渠底
,其中渠底![]() 宽为1米,渠口
宽为1米,渠口![]() 宽为3米,渠深
宽为3米,渠深![]() 米.根据国家对农田建设补贴的政策,该农场计划在原水渠的基础上分别沿射线
米.根据国家对农田建设补贴的政策,该农场计划在原水渠的基础上分别沿射线![]() 方向加宽、
方向加宽、![]() 方向加深,若扩建后的水渠横截面
方向加深,若扩建后的水渠横截面![]() 仍是等腰梯形,且面积是原面积的2倍.设扩建后渠深为
仍是等腰梯形,且面积是原面积的2倍.设扩建后渠深为![]() 米,若挖掘费用为每立方米
米,若挖掘费用为每立方米![]() 万元,水渠的内壁(渠底和梯形两腰,
万元,水渠的内壁(渠底和梯形两腰,![]() 端也要重新铺设)铺设混凝土的费用为每平方米
端也要重新铺设)铺设混凝土的费用为每平方米![]() 万元.
万元.
(1)用![]() 表示渠底
表示渠底![]() 的长度,并求出
的长度,并求出![]() 的取值范围;
的取值范围;
(2)问渠深![]() 为多少米时,建设费用最低?
为多少米时,建设费用最低?
查看答案和解析>>
科目: 来源: 题型:
【题目】某生产基地有五台机器,现有五项工作待完成,每台机器完成每项工作后获得的效益值如表所示.若每台机器只完成一项工作,且完成五项工作后获得的效益值总和最大,则下列叙述错误的的是_____________.
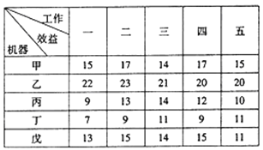
①甲只能承担第四项工作
②乙不能承担第二项工作
③丙可以不承担第三项工作
④丁可以承担第三项工作
查看答案和解析>>
科目: 来源: 题型:
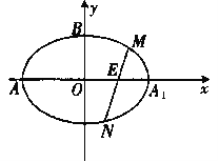
【题目】如图,在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,点
,点![]() 分别为椭圆
分别为椭圆![]() 与坐标轴的交点,且
与坐标轴的交点,且![]() .过
.过![]() 轴上定点
轴上定点![]() 的直线与椭圆
的直线与椭圆![]() 交于
交于![]() ,
,![]() 两点,点
两点,点![]() 为线段
为线段![]() 的中点.
的中点.
(1)求椭圆![]() 的方程;
的方程;
(2)求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】下列四个命题,其中正确的是( )
A.对分类变量![]() 与
与![]() 的随机变量
的随机变量![]() 的观测值
的观测值![]() 来说,
来说,![]() 越小,“
越小,“![]() 与
与![]() 有关系”可信程度越大
有关系”可信程度越大
B.残差点比较均匀地落在水平带状区域内,带状区域越窄,则模型拟合精度越高
C.相关指数![]() 越小,则残差平方和越大,模型的拟合效果越好
越小,则残差平方和越大,模型的拟合效果越好
D.两个随机变量相关性越强,则相关系数的绝对值越接近![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】曾玉、刘云、李梦、张熙四人被北京大学、清华大学、武汉大学和复旦大学录取,他们分别被哪个学校录取,同学们做了如下的猜想
甲同学猜:曾玉被武汉大学录取,李梦被复旦大学录取
同学乙猜:刘云被清华大学录取,张熙被北京大学录取
同学丙猜:曾玉被复旦大学录取,李梦被清华大学录取
同学丁猜:刘云被清华大学录取,张熙被武汉大学录取
结果,恰好有三位同学的猜想各对了一半,还有一位同学的猜想都不对
那么曾玉、刘云、李梦、张熙四人被录取的大小可能是( )
A.北京大学、清华大学、复旦大学、武汉大学
B.武汉大学、清华大学、复旦大学、北京大学
C.清华大学、北京大学、武汉大学 、复旦大学
D.武汉大学、复旦大学、清华大学、北京大学
查看答案和解析>>
科目: 来源: 题型:
【题目】已知在平面直角坐标系![]() 中,直线l的参数方程为
中,直线l的参数方程为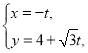 (
(![]() 为参数),曲线
为参数),曲线![]() 的方程为
的方程为![]() .以坐标原点
.以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.
(1)求直线l和曲线![]() 的极坐标方程;
的极坐标方程;
(2)曲线![]() 分别交直线和曲线
分别交直线和曲线![]() 于点
于点![]() ,求
,求![]() 的最大值及相应的
的最大值及相应的![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某校高一某班的某次数学测试成绩(满分为100分)的茎叶图和频率分布直方图都受了不同程度的破坏,但可见部分如图,据此解答下列问题:
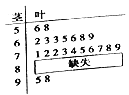
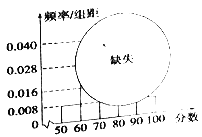
(1)求分数在![]() 的频率及全班人数;
的频率及全班人数;
(2)求分数在![]() 之间的频数,并计算频率分布直方图中
之间的频数,并计算频率分布直方图中![]() 间的矩形的高.
间的矩形的高.
(3)若从分数在![]() 和分数在90分以上的试卷选3份试卷进行试卷分析,求最高分的试卷被抽中的概率.
和分数在90分以上的试卷选3份试卷进行试卷分析,求最高分的试卷被抽中的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】某公司计划购买1台机器,该种机器使用三年后即被淘汰.在购进机器时,可以一次性额外购买几次维修服务,每次维修服务费用200元,另外实际维修一次还需向维修人员支付小费,小费每次50元.在机器使用期间,如果维修次数超过购机时购买的维修服务次数,则每维修一次需支付维修服务费用500元,无需支付小费.现需决策在购买机器时应同时一次性购买几次维修服务,为此搜集并整理了100台这种机器在三年使用期内的维修次数,得下面统计表:
维修次数 | 8 | 9 | 10 | 11 | 12 |
频数 | 10 | 20 | 30 | 30 | 10 |
记![]() 表示1台机器在三年使用期内的维修次数,
表示1台机器在三年使用期内的维修次数,![]() 表示1台机器在维修上所需的费用(单位:元),
表示1台机器在维修上所需的费用(单位:元),![]() 表示购机的同时购买的维修服务次数.
表示购机的同时购买的维修服务次数.
(1)若![]() ,求
,求![]() 与
与![]() 的函数解析式;
的函数解析式;
(2)若要求“维修次数不大于![]() ”的频率不小于0.8,求
”的频率不小于0.8,求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com