
科目: 来源: 题型:
| 3 |

查看答案和解析>>
科目: 来源: 题型:
 如图,在△ABC中,∠BAC=90°,AD是BC边上的高,E是BC边上的一个动点(不与B,C重合),EF⊥AB,EG⊥AC,垂足分别为F,G.
如图,在△ABC中,∠BAC=90°,AD是BC边上的高,E是BC边上的一个动点(不与B,C重合),EF⊥AB,EG⊥AC,垂足分别为F,G.| EG |
| AD |
| CG |
| CD |
查看答案和解析>>
科目: 来源: 题型:
 23、如图,在△ABC中,D为AC上一点,CD=2DA,∠BAC=45°,∠BDC=60°,CE⊥BD,E为垂足,连接AE.
23、如图,在△ABC中,D为AC上一点,CD=2DA,∠BAC=45°,∠BDC=60°,CE⊥BD,E为垂足,连接AE.查看答案和解析>>
科目: 来源: 题型:
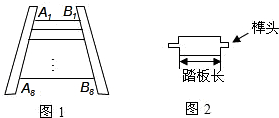 需要买几块这样的木板?请说明理由.(不考虑锯缝的损耗)
需要买几块这样的木板?请说明理由.(不考虑锯缝的损耗)查看答案和解析>>
科目: 来源: 题型:
| ||
| 2 |
查看答案和解析>>
科目: 来源: 题型:
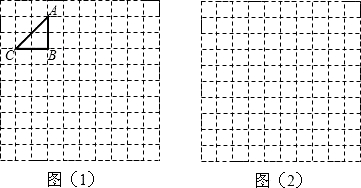
 如图是一个边长为1的正方形组成的网络,△ABC与△A1B1C1都是格点三角形(顶点在网格交点处),并且△ABC∽△A1B1C1,则△ABC与△A1B1C1的相似比是
如图是一个边长为1的正方形组成的网络,△ABC与△A1B1C1都是格点三角形(顶点在网格交点处),并且△ABC∽△A1B1C1,则△ABC与△A1B1C1的相似比是查看答案和解析>>
科目: 来源: 题型:
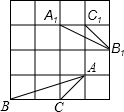
 17、如图,对面积为1的△ABC逐次进行以下操作:第一次操作,分别延长AB,BC,CA至点A1,B1,C1,使得A1B=2AB,B1C=2BC,C1A=2CA,顺次连接A1,B1,C1,得到△A1B1C1,记其面积为S1;第二次操作,分别延长A1B1,B1C1,C1A1至点A2,B2,C2,使得A2B1=2A1B1,B2C1=2B1C1,C2A1=2C1A1,顺次连接A2,B2,C2,得到△A2B2C2,记其面积为S2;…;按此规律继续下去,可得到△A5B5C5,则其面积S5=
17、如图,对面积为1的△ABC逐次进行以下操作:第一次操作,分别延长AB,BC,CA至点A1,B1,C1,使得A1B=2AB,B1C=2BC,C1A=2CA,顺次连接A1,B1,C1,得到△A1B1C1,记其面积为S1;第二次操作,分别延长A1B1,B1C1,C1A1至点A2,B2,C2,使得A2B1=2A1B1,B2C1=2B1C1,C2A1=2C1A1,顺次连接A2,B2,C2,得到△A2B2C2,记其面积为S2;…;按此规律继续下去,可得到△A5B5C5,则其面积S5=查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com