
科目: 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线C的参数方程为:![]() (
(![]() 为参数,已知直线
为参数,已知直线![]() ,直线
,直线![]() 以坐标原点为极点,x轴正半轴为极轴,建立极坐标系.
以坐标原点为极点,x轴正半轴为极轴,建立极坐标系.
(1)求曲线C以及直线![]() ,
,![]() 的极坐标方程;
的极坐标方程;
(2)若直线![]() 与曲线C分别交于O、A两点,直线
与曲线C分别交于O、A两点,直线![]() 与曲线C分别交于O、B两点,求
与曲线C分别交于O、B两点,求![]() 的面积.
的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)![]() x2+ax+lnx(a∈R)
x2+ax+lnx(a∈R)
(1)讨论函数f(x)的单调性;
(2)若f(x)存在两个极值点x1,x2且|x1﹣x2|![]() ,求|f(x1)﹣f(x2)|的最大值.
,求|f(x1)﹣f(x2)|的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆C的中心在坐标原点O,其右焦点为F(1,0),以坐标原点O为圆心,椭圆短半轴长为半径的圆与直线x﹣y![]() 0的相切.
0的相切.
(1)求椭圆C的方程;
(2)经过点F的直线l1,l2分别交椭圆C于A、B及C、D四点,且l1⊥l2,探究:是否存在常数λ,使![]() 恒成立.
恒成立.
查看答案和解析>>
科目: 来源: 题型:
【题目】为评估设备![]() 生产某种零件的性能,从设备
生产某种零件的性能,从设备![]() 生产该零件的流水线上随机抽取100个零件为样本,测量其直径后,整理得到下表:
生产该零件的流水线上随机抽取100个零件为样本,测量其直径后,整理得到下表:
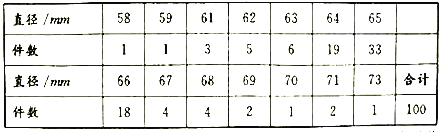
经计算,样本的平均值![]() ,标准差
,标准差![]() ,以频率值作为概率的估计值.
,以频率值作为概率的估计值.
(I)为评判一台设备的性能,从该设备加工的零件中任意抽取一件,记其直径为![]() ,并根据以下不等式进行判定(
,并根据以下不等式进行判定(![]() 表示相应事件的概率):
表示相应事件的概率):
①![]() ;
;
②![]() ;
;
③![]() .
.
判定规则为:若同时满足上述三个式子,则设备等级为甲;若仅满足其中两个,则等级为乙,若仅满足其中一个,则等级为丙;若全部都不满足,则等级为了.试判断设备![]() 的性能等级.
的性能等级.
(Ⅱ)将直径尺寸在![]() 之外的零件认定为是“次品”.
之外的零件认定为是“次品”.
①从设备![]() 的生产流水线上随机抽取2个零件,求其中次品个数
的生产流水线上随机抽取2个零件,求其中次品个数![]() 的数学期望
的数学期望![]() ;
;
②从样本中随意抽取2个零件,求其中次品个数![]() 的数学期望
的数学期望![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】在四棱锥P﹣ABCD中,平面PAC⊥平面ABCD,且有AB∥DC,AC=CD=DA![]() AB.
AB.

(1)证明:BC⊥PA;
(2)若PA=PC=AC,求平面PAD与平面PBC所成的锐二面角的余弦值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知Sn为数列{an}的前n项和,且Sn+2=2an,n∈N*.
(1)求数列{an}的通项公式;
(2)令bn![]() ,设数列{bn}的前项和为Tn,若Tn
,设数列{bn}的前项和为Tn,若Tn![]() ,求n的最小值.
,求n的最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】直线l:x﹣ty+1=0(t>0)和抛物线C:y2=4x相交于不同两点A、B,设AB的中点为M,抛物线C的焦点为F,以MF为直径的圆与直线l相交另一点为N,且满足|MN|![]() |NF|,则直线l的方程为_____.
|NF|,则直线l的方程为_____.
查看答案和解析>>
科目: 来源: 题型:
【题目】“新冠肺炎”爆发后,某医院由甲、乙、丙、丁、戊5位医生组成的专家组到某市参加抗击疫情.五位医生去乘高铁,按规定每位乘客在进站前都需要安检,当时只有3个安检口开通,且没有其他旅客进行安检.5位医生分别从3个安检口进行安检,每个安检口都有医生去安检且不同的安检顺序视为不同的安检,则甲、乙2位医生不在同一个安检口进行安检的概率为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com