
科目: 来源: 题型:
查看答案和解析>>
科目: 来源: 题型:
查看答案和解析>>
科目: 来源: 题型:
 操作:正方体涂色:如图,用白萝卜做成一个正方体,并把正方体表面涂成灰颜色.
操作:正方体涂色:如图,用白萝卜做成一个正方体,并把正方体表面涂成灰颜色.查看答案和解析>>
科目: 来源: 题型:
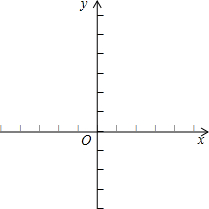 ,0),与y轴负半轴交于点C,其对称轴是直线x=
,0),与y轴负半轴交于点C,其对称轴是直线x=| 3 | 2 |
查看答案和解析>>
科目: 来源: 题型:
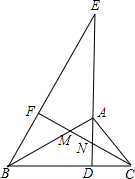 已知,如图,AD为Rt△ABC斜边BC上的高,点E为DA延长线上一点,连接BE,过点C作CF⊥BE于点F,交AB、AD于M、N两点.
已知,如图,AD为Rt△ABC斜边BC上的高,点E为DA延长线上一点,连接BE,过点C作CF⊥BE于点F,交AB、AD于M、N两点.| 5 |
| 4 |
| 15 |
| 8 |
| 9 |
| 8 |
查看答案和解析>>
科目: 来源: 题型:
查看答案和解析>>
科目: 来源: 题型:
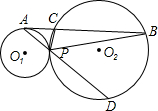 线AP交圆O2于点D,连接DC、PC.
线AP交圆O2于点D,连接DC、PC.| 6 |
查看答案和解析>>
科目: 来源: 题型:
 25、某中学为了了解全校1000名学生参加课外锻炼的情况,从中抽查了50名学生一周内平均每天参加课外锻炼的时间(单位为分钟,且取整数),将抽查得到的数据进行适当整理,分成5组(第1小组是10.5-20.5,第2小组是20.5-30.5,第3小组是30.5-40.5,第4小组是40.5-50.5,第5小组是50.5-60.5),列出了下面未完成的频率分布表.
25、某中学为了了解全校1000名学生参加课外锻炼的情况,从中抽查了50名学生一周内平均每天参加课外锻炼的时间(单位为分钟,且取整数),将抽查得到的数据进行适当整理,分成5组(第1小组是10.5-20.5,第2小组是20.5-30.5,第3小组是30.5-40.5,第4小组是40.5-50.5,第5小组是50.5-60.5),列出了下面未完成的频率分布表.查看答案和解析>>
科目: 来源: 题型:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com