
科目: 来源: 题型:
【题目】已知曲线Cn:x2﹣2nx+y2=0,(n=1,2,…).从点P(﹣1,0)向曲线Cn引斜率为kn(kn>0)的切线ln,切点为Pn(xn,yn).
(1)求数列{xn}与{yn}的通项公式;
(2)证明: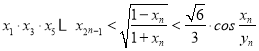 .
.
查看答案和解析>>
科目: 来源: 题型:
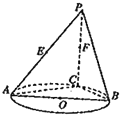
【题目】如图,AB是圆O的直径,点C是圆O上异于A,B的点,直线PC⊥平面ABC,E,F分别是PA,PC的中点.
(1)记平面BEF与平面ABC的交线为l,试判断直线l与平面PAC的位置关系,并加以证明;
(2)设(1)中的直线l与圆O的另一个交点为D,且点Q满足![]() .记直线PQ与平面ABC所成的角为θ,异面直线PQ与EF所成的角为α,二面角E﹣l﹣C的大小为β.求证:sinθ=sinαsinβ.
.记直线PQ与平面ABC所成的角为θ,异面直线PQ与EF所成的角为α,二面角E﹣l﹣C的大小为β.求证:sinθ=sinαsinβ.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知数列{an}是等差数列,Sn为{an}的前n项和,且a10=19,S10=100;数列{bn}对任意n∈N*,总有b1![]() b2
b2![]() b3…bn﹣1
b3…bn﹣1![]() bn=an+2成立.
bn=an+2成立.
(1)求数列{an}和{bn}的通项公式;
(2)记cn=(﹣1)n![]() ,求数列{cn}的前n项和Tn.
,求数列{cn}的前n项和Tn.
查看答案和解析>>
科目: 来源: 题型:
【题目】某蛋糕店制作并销售一款蛋糕,制作一个蛋糕成本3元,且以8元的价格出售,若当天卖不完,剩下的则无偿捐献给饲料加工厂。根据以往100天的资料统计,得到如下需求量表。该蛋糕店一天制作了这款蛋糕![]() 个,以
个,以![]() (单位:个,
(单位:个,![]() ,
,![]() )表示当天的市场需求量,
)表示当天的市场需求量,![]() (单位:元)表示当天出售这款蛋糕获得的利润.
(单位:元)表示当天出售这款蛋糕获得的利润.
需求量/个 |
|
|
|
|
|
天数 | 15 | 25 | 30 | 20 | 10 |
(1)当![]() 时,若
时,若![]() 时获得的利润为
时获得的利润为![]() ,
,![]() 时获得的利润为
时获得的利润为![]() ,试比较
,试比较![]() 和
和![]() 的大小;
的大小;
(2)当![]() 时,根据上表,从利润
时,根据上表,从利润![]() 不少于570元的天数中,按需求量分层抽样抽取6天.
不少于570元的天数中,按需求量分层抽样抽取6天.
(i)求此时利润![]() 关于市场需求量
关于市场需求量![]() 的函数解析式,并求这6天中利润为650元的天数;
的函数解析式,并求这6天中利润为650元的天数;
(ii)再从这6天中抽取3天做进一步分析,设这3天中利润为650元的天数为![]() ,求随机变量
,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平行四边形ABCD中,AB=1,AD![]() ,且∠BAD=45°,以BD为折线,把△ABD折起,使AB⊥DC,连接AC,得到三棱锥A﹣BCD.
,且∠BAD=45°,以BD为折线,把△ABD折起,使AB⊥DC,连接AC,得到三棱锥A﹣BCD.
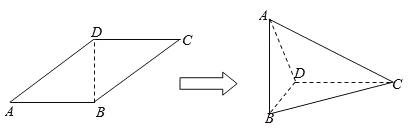
(1)求证:平面ABD⊥平面BCD;
(2)求二面角B﹣AC﹣D的大小.
查看答案和解析>>
科目: 来源: 题型:
【题目】△ABC的内角A,B,C的对边分别为a,b,c,已知△ABC的面积为![]()
(1)求sinBsinC;
(2)若6cosBcosC=1,a=3,求△ABC的周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com